题目内容
已知正四面体ABCD的表面积为S,其四个面的中心分别为E、F、G、H.设四面体EFGH的表面积为T,则
等于( )
| T |
| S |
A、
| ||
B、
| ||
C、
| ||
D、
|
分析:因为正四面体四个面都是正△,其中心到顶点的距离等于到对边距离的一半,通过作出辅助线,可得两四面体的边长比,由面积比是边长比的平方,可得出答案.
解答: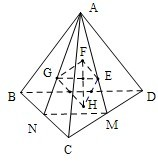 解:如图所示,正四面体ABCD四个面的中心分别为E、F、G、H,
解:如图所示,正四面体ABCD四个面的中心分别为E、F、G、H,
∴四面体EFGH也是正四面体.
连接AE并延长与CD交于点M,
连接AG并延长与BC交于点N.
∵E、G分别为面的中心,
∴
=
=
.∴
=
.
又∵MN=
BD,∴
=
.
∵面积比是相似比的平方,∴两四面体的面积比为;
=
.
故答案为:A
 解:如图所示,正四面体ABCD四个面的中心分别为E、F、G、H,
解:如图所示,正四面体ABCD四个面的中心分别为E、F、G、H,∴四面体EFGH也是正四面体.
连接AE并延长与CD交于点M,
连接AG并延长与BC交于点N.
∵E、G分别为面的中心,
∴
| AE |
| AM |
| AG |
| AN |
| 2 |
| 3 |
| GE |
| MN |
| 2 |
| 3 |
又∵MN=
| 1 |
| 2 |
| GE |
| BD |
| 1 |
| 3 |
∵面积比是相似比的平方,∴两四面体的面积比为;
| T |
| S |
| 1 |
| 9 |
故答案为:A
点评:本题考查了多面体的面积比是边长比的平方,本题关键是求边长比是多少;类似的有体积比是边长比的立方,三角形的高,中线,角平分线的比等于边长的比.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 已知正四面体ABCD中,M、N分别是BC和AD中点,则异面直线AM和CN所成的角的正切值为( )
已知正四面体ABCD中,M、N分别是BC和AD中点,则异面直线AM和CN所成的角的正切值为( )