题目内容
已知函数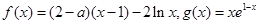 ,(
,( 为自然对数的底数)。
为自然对数的底数)。
(1)当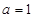 时,求函数
时,求函数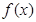 在区间
在区间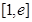 上的最大值和最小值;
上的最大值和最小值;
(2)若对任意给定的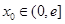 ,在
,在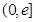 上总存在两个不同的
上总存在两个不同的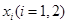 ,使得
,使得 成立,求
成立,求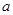 的取值范围。
的取值范围。
【答案】
(1)最大值为0,最小值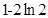 。(2)
。(2)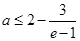 。
。
【解析】
试题分析:(1)当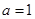 时,
时,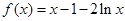 ,
,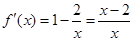 ,…………2分
,…………2分
则函数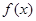 在区间
在区间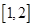 上为减函数,在区间
上为减函数,在区间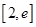 上为增函数,……………
上为增函数,……………
又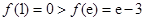 ,则
,则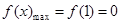 , ………………5分
, ………………5分
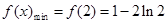 。 …………………6分
。 …………………6分
(2)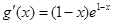 ,则函数
,则函数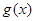 在区间
在区间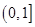 上为增函数,在区间
上为增函数,在区间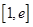 上为减函数,
上为减函数,
又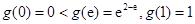 ,则函数
,则函数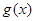 的值域为
的值域为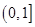 。………………8分
。………………8分
则转化为:当 时,
时,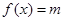 在区间
在区间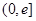 上有两个不同的根。…………9分
上有两个不同的根。…………9分
而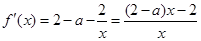 。
。
当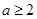 时,函数
时,函数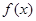 在区间
在区间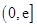 上为减函数,不符合题意。…………………10分
上为减函数,不符合题意。…………………10分
当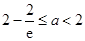 时,有
时,有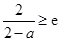 ,函数
,函数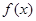 在区间
在区间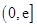 上为减函数,
上为减函数,
不符合题意。 ………………………11分
当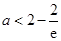 时,有
时,有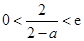 ,此时函数
,此时函数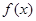 在区间
在区间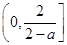 上为减函数,在区间
上为减函数,在区间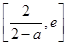 上为增函数,而当
上为增函数,而当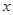 趋于零时,
趋于零时,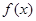 趋于正无穷,且最小值为
趋于正无穷,且最小值为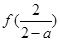 。
。
要使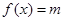 在区间
在区间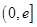 上有两个不同的根,则
上有两个不同的根,则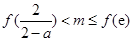 。 ………12分
。 ………12分
又 ,且
,且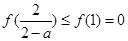 ,故只要
,故只要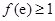 ,得
,得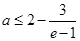 。
。
而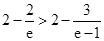 ,从而有
,从而有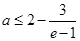 。 ……14分
。 ……14分
考点:利用导数研究函数的单调区间和最值;导数的综合应用。
点评:在高考中,重点考查利用导数研究函数的单调性,求单调区间、极值、最值,以及利用导数解决生活中的优化问题。多以解答题的形式出现,属于中、高档题目。

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
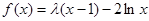 ,
, ,(
,( 为自然对数的底数).
为自然对数的底数). 时,求函数
时,求函数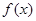 的单调区间;
的单调区间;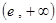 上恒为正数,求
上恒为正数,求 的最小值;
的最小值;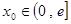 ,在
,在 上总存在两个不同的
上总存在两个不同的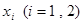 ,使得
,使得 成立,求
成立,求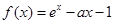 (
(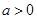 ,
,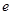 为自然对数的底数).
为自然对数的底数).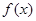 的最小值;
的最小值;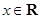 恒成立,求实数
恒成立,求实数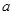 的值;
的值;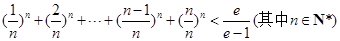
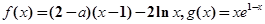 ,(
,(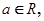 e为自然对数的底数)
e为自然对数的底数)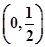 上无零点,求a的最小值;
上无零点,求a的最小值;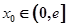 ,在
,在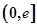 上总存在两个不同的
上总存在两个不同的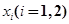 ,使得
,使得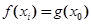 成立,求a的取值范围.
成立,求a的取值范围.