题目内容
已知 ≤a≤1,若f(x)=ax2-2x+1在区间[1,3]上的最大值M(a),最小值N(a),设g(a)=M(a)-N(a).
≤a≤1,若f(x)=ax2-2x+1在区间[1,3]上的最大值M(a),最小值N(a),设g(a)=M(a)-N(a).(1)求g(a)的解析式;
(2)判断g(a)单调性,求g(a)的最小值.
【答案】分析:(1)根据已知条件a>0,知函数是二次函数,其图象是开口向上的抛物线.因此讨论对称轴:x=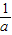 与区间[1,3]的关系,得到函数的单调性后再找出相应的最值,即可得g(a)的解析式;
与区间[1,3]的关系,得到函数的单调性后再找出相应的最值,即可得g(a)的解析式;
(2)通过求导数,讨论其正负,可得到函数g(a)在区间[ ,
, ]上单调减,而在(
]上单调减,而在( ,1]上单调增,因此不难得出
,1]上单调增,因此不难得出
g(a)的最小值为g( )=
)= .
.
解答:解:(1)当 ≤a≤
≤a≤ 时N(a)=f(
时N(a)=f( ),M(a)=f(1),
),M(a)=f(1),
此时g(a)=f(1)-f(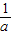 )=a+
)=a+ -2;
-2;
当 <a≤1时N(a)=f(
<a≤1时N(a)=f( ),M(a)=f(3),
),M(a)=f(3),
此时g(a)=f(3)-f( )=9a+
)=9a+ -6;
-6;
∴g(a)=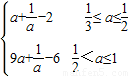 …(6分)
…(6分)
(2)当 ≤a≤
≤a≤ 时,∵g(a)=a+
时,∵g(a)=a+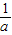 -2,∴g′(a)=1-
-2,∴g′(a)=1- <0,
<0,
∴g(a)在[ ,
, ]上单调递减.
]上单调递减.
同理可知g(a)在( ,1]上单调递增
,1]上单调递增
∴g(a)min=g( )=
)= .…(12分)
.…(12分)
点评:本题考查了二次函数在闭区间上的最值问题,属于基础题.研究二次函数的最值的关键是用其图象,或用导数研究它的单调性.
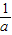 与区间[1,3]的关系,得到函数的单调性后再找出相应的最值,即可得g(a)的解析式;
与区间[1,3]的关系,得到函数的单调性后再找出相应的最值,即可得g(a)的解析式;(2)通过求导数,讨论其正负,可得到函数g(a)在区间[
 ,
, ]上单调减,而在(
]上单调减,而在( ,1]上单调增,因此不难得出
,1]上单调增,因此不难得出g(a)的最小值为g(
 )=
)= .
.解答:解:(1)当
 ≤a≤
≤a≤ 时N(a)=f(
时N(a)=f( ),M(a)=f(1),
),M(a)=f(1),此时g(a)=f(1)-f(
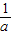 )=a+
)=a+ -2;
-2;当
 <a≤1时N(a)=f(
<a≤1时N(a)=f( ),M(a)=f(3),
),M(a)=f(3),此时g(a)=f(3)-f(
 )=9a+
)=9a+ -6;
-6;∴g(a)=
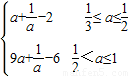 …(6分)
…(6分)(2)当
 ≤a≤
≤a≤ 时,∵g(a)=a+
时,∵g(a)=a+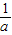 -2,∴g′(a)=1-
-2,∴g′(a)=1- <0,
<0,∴g(a)在[
 ,
, ]上单调递减.
]上单调递减.同理可知g(a)在(
 ,1]上单调递增
,1]上单调递增∴g(a)min=g(
 )=
)= .…(12分)
.…(12分)点评:本题考查了二次函数在闭区间上的最值问题,属于基础题.研究二次函数的最值的关键是用其图象,或用导数研究它的单调性.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ≤a≤1,若f(x)=ax2-2x+1在区间[1,3]上的最大值M(a),最小值N(a),设g(a)=M(a)-N(a).
≤a≤1,若f(x)=ax2-2x+1在区间[1,3]上的最大值M(a),最小值N(a),设g(a)=M(a)-N(a). ≤a≤1,若f(x)=ax2-2x+1在区间[1,3]上的最大值M(a),最小值N(a),设g(a)=M(a)-N(a).
≤a≤1,若f(x)=ax2-2x+1在区间[1,3]上的最大值M(a),最小值N(a),设g(a)=M(a)-N(a). ≤a≤1,若f(x)=ax2-2x+1在区间[1,3]上的最大值M(a),最小值N(a),设g(a)=M(a)-N(a).
≤a≤1,若f(x)=ax2-2x+1在区间[1,3]上的最大值M(a),最小值N(a),设g(a)=M(a)-N(a). ≤a≤1,若f(x)=ax2-2x+1在区间[1,3]上的最大值M(a),最小值N(a),设g(a)=M(a)-N(a).
≤a≤1,若f(x)=ax2-2x+1在区间[1,3]上的最大值M(a),最小值N(a),设g(a)=M(a)-N(a).