题目内容
若函数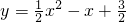 的定义域和值域都是[1,b],则实数b的值为
的定义域和值域都是[1,b],则实数b的值为
- A.2
- B.3
- C.4
- D.5
B
分析:先将二次函数进行配方,得到抛物线的对称轴,利用定义域和对称轴之间的关系,建立方程,可求b.
解答:数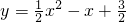 =
=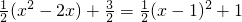 ,抛物线的对称轴为x=1,
,抛物线的对称轴为x=1,
因为定义域为[1,b],所以函数在[1,b]上单调递增,
因为定义域和值域都是[1,b],
所以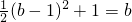 ,解得b=3或b=1(舍去).
,解得b=3或b=1(舍去).
故选B.
点评:本题主要考查二次函数的图象和性质.利用配方先得到函数的对称轴,是解决本题的关键.
分析:先将二次函数进行配方,得到抛物线的对称轴,利用定义域和对称轴之间的关系,建立方程,可求b.
解答:数
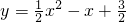 =
=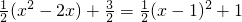 ,抛物线的对称轴为x=1,
,抛物线的对称轴为x=1,因为定义域为[1,b],所以函数在[1,b]上单调递增,
因为定义域和值域都是[1,b],
所以
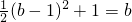 ,解得b=3或b=1(舍去).
,解得b=3或b=1(舍去).故选B.
点评:本题主要考查二次函数的图象和性质.利用配方先得到函数的对称轴,是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的定义域和值域均为
的定义域和值域均为 ,则
,则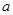 的范围是________.
的范围是________. 的定义域和值域都是[0,1],则a=( )
的定义域和值域都是[0,1],则a=( ) C.
C. D.
D.
 的定义域和值域都是
的定义域和值域都是 ,则实数
,则实数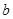 的值为 ( )
的值为 ( )