题目内容

以点（±3，0）为焦点，且渐近线为 $数学公式$ 的双曲线标准方程是________．

$\text{[math]}$
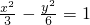
分析：利用双曲线的焦点在x轴时渐近线的方程 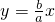$\text{[math]}$ 及双曲线中c²=a²+b²，列出方程组求出a，b的值，求出双曲线的方程．
解答：设双曲线的方程为 $\text{[math]}$
∵（±3，0）为焦点
∴c=3
∵渐近线为 $\text{[math]}$
∴ $\text{[math]}$
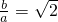
∵c²=a²+b²
所以有 $\text{[math]}$
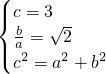
解得a=3，b=6
∴ $\text{[math]}$
故答案为 $\text{[math]}$
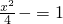
点评：本题考查利用待定系数法求双曲线的方程、考查双曲线三参数的关系c²=a²+b²．

练习册系列答案

榜上有名测评创新系列答案

蓉城学堂课前阅读系列答案

课内课外直通车系列答案

高中优等生一课一练系列答案

一通百通核心测考卷系列答案

衡水示范高中假期伴学出彩方案光明日报出版社系列答案

高中同步检测优化训练高效作业系列答案

课堂在线系列答案

同步大冲关系列答案

状元桥优质课堂系列答案

相关题目

（文科做）已知点A₁（2，0），A₂（1，t），A₃（0，b），A₄（-1，t），A₅（-2，0），其中t＞0，b为正常数．
（1）半径为2的圆C₁经过A_i（i=1，2，…，5）这五个点，求b和t的值；
（2）椭圆C₂以F₁（-c，0），F₂（c，0）（c＞0）为焦点，长轴长是4．若A_iF₁+A_iF₂=4（i=1，2，…，5），试用b表示t；
（3）在（2）中的椭圆C₂中，两线段长的差A₁F₁-A₁F₂，A₂F₁-A₂F₂，…，A₅F₁-A₅F₂构成一个数列{a_n}，求证：对n=1，2，3，4都有a_n+1＜a_n．（本小题解答中用到了椭圆的第一定义与焦半径公式，新教材实验区的学生可不解第三小题，请学习时注意）

（文科做）已知点A₁（2，0），A₂（1，t），A₃（0，b），A₄（-1，t），A₅（-2，0），其中t＞0，b为正常数．
（1）半径为2的圆C₁经过A_i（i=1，2，…，5）这五个点，求b和t的值；
（2）椭圆C₂以F₁（-c，0），F₂（c，0）（c＞0）为焦点，长轴长是4．若A_iF₁+A_iF₂=4（i=1，2，…，5），试用b表示t；
（3）在（2）中的椭圆C₂中，两线段长的差A₁F₁-A₁F₂，A₂F₁-A₂F₂，…，A₅F₁-A₅F₂构成一个数列{a_n}，求证：对n=1，2，3，4都有a_n+1＜a_n．（本小题解答中用到了椭圆的第一定义与焦半径公式，新教材实验区的学生可不解第三小题，请学习时注意）

（文科做）已知点A₁（2，0），A₂（1，t），A₃（0，b），A₄（-1，t），A₅（-2，0），其中t＞0，b为正常数．
（1）半径为2的圆C₁经过A_i（i=1，2，…，5）这五个点，求b和t的值；
（2）椭圆C₂以F₁（-c，0），F₂（c，0）（c＞0）为焦点，长轴长是4．若A_iF₁+A_iF₂=4（i=1，2，…，5），试用b表示t；
（3）在（2）中的椭圆C₂中，两线段长的差A₁F₁-A₁F₂，A₂F₁-A₂F₂，…，A₅F₁-A₅F₂构成一个数列{a_n}，求证：对n=1，2，3，4都有a_n+1＜a_n．（本小题解答中用到了椭圆的第一定义与焦半径公式，新教材实验区的学生可不解第三小题，请学习时注意）