题目内容
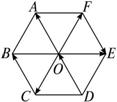
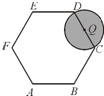如图，在边长为2的正六边形ABCDEF中，动圆Q的半径为1，圆心在线段CD（含端点）上运动，P是圆Q上及内部的动点，设向量| AP |
| AB |
| AF |
| A、（1，2] |
| B、[5，6] |
| C、[2，5] |
| D、[3，5] |
分析：如图所示，设点O为正六边形的中心，则
=
+
，当动圆Q的圆心经过点C时，与边BC交于点P，点P为边BC的中点．连接OP，可知
=
+
，利用共线定理可得：存在实数t，使得
=t
．于是
=
+t
=(1+t)
+(1-t)
，此时m+n=2，取得最小值．当动圆Q的圆心经过点D时，取AD的延长线与⊙Q的交点P时．
=
=
(
+
)=
+
，此时m+n=5取得最大值．
| AO |
| AB |
| AF |
| AP |
| AO |
| OP |
| OP |
| FB |
| AP |
| AO |
| FB |
| AB |
| AF |
| AP |
| 5 |
| 2 |
| AO |
| 5 |
| 2 |
| AB |
| AF |
| 5 |
| 2 |
| AB |
| 5 |
| 2 |
| AF |
解答：解：如图所示，
①设点O为正六边形的中心，则
=
+
．
当动圆Q的圆心经过点C时，与边BC交于点P，点P为边BC的中点．连接OP，
则
=
+
，
∵
与
共线，∴存在实数t，使得
=t
．
∴
=
+t
=
+
+t(
-
)=(1+t)
+(1-t)
，
此时m+n=1+t+1-t=2，取得最小值．
②当动圆Q的圆心经过点D时，取AD的延长线与⊙Q的交点P时．
=
=
(
+
)=
+
，
此时m+n=
+
=5取得最大值．
因此m+n的取值范围是[2，5]．
故选：C．
①设点O为正六边形的中心，则
| AO |
| AB |
| AF |
当动圆Q的圆心经过点C时，与边BC交于点P，点P为边BC的中点．连接OP，
则
| AP |
| AO |
| OP |
∵
| OP |
| FB |
| OP |
| FB |
∴
| AP |
| AO |
| FB |
| AB |
| AF |
| AB |
| AF |
| AB |
| AF |
此时m+n=1+t+1-t=2，取得最小值．
②当动圆Q的圆心经过点D时，取AD的延长线与⊙Q的交点P时．
| AP |
| 5 |
| 2 |
| AO |
| 5 |
| 2 |
| AB |
| AF |
| 5 |
| 2 |
| AB |
| 5 |
| 2 |
| AF |
此时m+n=
| 5 |
| 2 |
| 5 |
| 2 |
因此m+n的取值范围是[2，5]．
故选：C．
点评：本题考查了向量的平行四边形法则、向量的运算、平面向量的基本定理、正六边形的性质等基础知识与基本技能方法，属于难题．
练习册系列答案
相关题目
（2013•资阳模拟）如图，在边长为2的正六边形ABCDEF中，P是△CDE内（含边界）的动点，设向量
的起点、终点和模;
共线的向量;
相等的向量.