题目内容
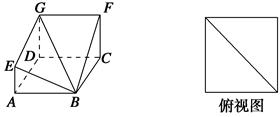
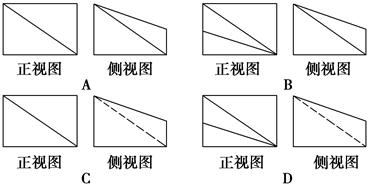
如图⑴、⑵、⑶、⑷为四个几何体的三视图,根据三视图可以判断这四个几何体依次分别为( )
| A.三棱台、三棱柱、圆锥、圆台 | B.三棱台、三棱锥、圆锥、圆台 |
| C.三棱柱、正四棱锥、圆锥、圆台 | D.三棱柱、三棱台、圆锥、圆台 |
C
解析试题分析:图(1)中正视图是一个矩形,俯视图是两个全等的矩形,而左视图是一个正三角形,该几何体是平放的三棱柱;图(2)(3)的正视图、侧视图都是两个全等的等腰三角形,但图(2)的俯视图是的个带对角线的正方形,该几何体应的正四棱锥;图(3)的俯视图是个带心的圆,对应的几何体应是圆锥;最后图(4)的正视图、侧视图是两个全等的等腰梯形,俯视图是两个同心圆,这正月是圆台的特征.故选C.
考点:1、简单几何体的结构特征;2、棱柱、棱锥、圆锥、圆台的三视图.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
某几何体的三视图如图所示,则该几何体的体积为( )
A. | B. | C. | D. |
某三棱锥的三视图如图所示,该三棱锥的体积为( )
A. | B. | C. | D. |
已知某几何体的三视图如图,则该几何体的体积是( )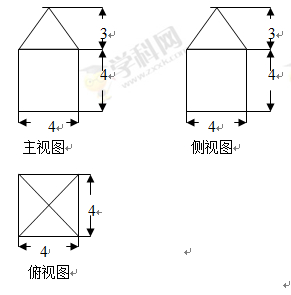
A.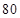 | B.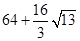 | C.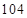 | D.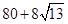 |
某三棱椎的三视图如图所示,该三棱锥的四个面的面积中,最大的是( )
A. | B. | C. | D.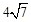 |
如图所示是一个几何体的三视图,若该几何体的体积为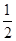 ,则主视图中三角形的高x的值为( )
,则主视图中三角形的高x的值为( )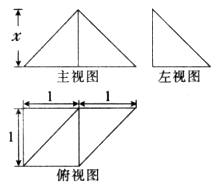
A.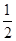 | B.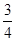 | C.1 | D.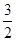 |
将一个等腰梯形绕着它的较长的底边所在的直线旋转一周,所得的几何体包括( )
| A.一个圆台、两个圆锥 | B.一个圆柱、两个圆锥 |
| C.两个圆台、一个圆柱 | D.两个圆柱、一个圆台 |
 的底面是正三角形,各条侧棱均相等,
的底面是正三角形,各条侧棱均相等,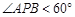 . 设点
. 设点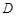 、
、 分别在线段
分别在线段 、
、 上,且
上,且 ,记
,记 ,
, 周长为
周长为 ,则
,则 的图象可能是( )
的图象可能是( )