题目内容
已知椭圆E: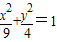 及点M(1,1).
及点M(1,1).(1)直线l过点M与椭圆E相交于A,B两点,求当点M为弦AB中点时的直线l方程;
(2)直线l过点M与椭圆E相交于A,B两点,求弦AB的中点轨迹;
(3)(文)斜率为2的直线l与椭圆E相交于A,B两点,求弦AB的中点轨迹.
(3)(理)若椭圆E上存在两点A,B关于直线l:y=2x+m对称,求m的取值范围.
【答案】分析:(1)设A(x1,y1),B(x2,y2),代入椭圆方程可得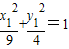 ,
,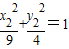 ,利用点差法及点M(1,1)为弦AB中点,即可求得点M为弦AB中点时的直线l方程;
,利用点差法及点M(1,1)为弦AB中点,即可求得点M为弦AB中点时的直线l方程;
(2)设弦AB的中点为(x,y),则由(1)知 ,从而可得弦AB的中点轨迹;
,从而可得弦AB的中点轨迹;
(3)(文)设弦AB的中点为(x,y),则由(1)知2= ,从而可得弦AB的中点轨迹;
,从而可得弦AB的中点轨迹;
(理)设A,B的中点M为(x,y),利用两点A,B关于直线l:y=2x+m对称,可得: ,利用点M必在椭圆内部,可求m的取值范围.
,利用点M必在椭圆内部,可求m的取值范围.
解答:解:(1)设A(x1,y1),B(x2,y2),代入椭圆方程可得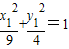 ,
,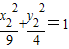
两式相减可得 =
=
∵点M(1,1)为弦AB中点,∴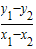 =-
=-
∴点M为弦AB中点时的直线l方程为y-1=- (x-1),即9y+4x-13=0
(x-1),即9y+4x-13=0
(2)设弦AB的中点为(x,y),则由(1)知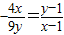 ,即9y2+4x2-9y-4x=0,∴弦AB的中点轨迹为椭圆;
,即9y2+4x2-9y-4x=0,∴弦AB的中点轨迹为椭圆;
(3)(文)设弦AB的中点为(x,y),则由(1)知2= ,即9y+2x=0,∴弦AB的中点轨迹为直线;
,即9y+2x=0,∴弦AB的中点轨迹为直线;
(理)设A,B的中点M为(x,y),kAB=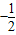 =
=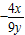 ①
①
又中点M在直线l:y=2x+m上,y=2x+m②
由①②得:
点M必在椭圆内部,所以有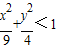
∴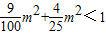
∴m2<4
解得:-2<m<2
点评:本题考查直线与圆锥曲线的综合,考查点差法的运用,考查对称性,解题的关键是正确运用点差法.
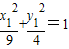 ,
,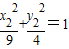 ,利用点差法及点M(1,1)为弦AB中点,即可求得点M为弦AB中点时的直线l方程;
,利用点差法及点M(1,1)为弦AB中点,即可求得点M为弦AB中点时的直线l方程;(2)设弦AB的中点为(x,y),则由(1)知
 ,从而可得弦AB的中点轨迹;
,从而可得弦AB的中点轨迹;(3)(文)设弦AB的中点为(x,y),则由(1)知2=
 ,从而可得弦AB的中点轨迹;
,从而可得弦AB的中点轨迹;(理)设A,B的中点M为(x,y),利用两点A,B关于直线l:y=2x+m对称,可得:
 ,利用点M必在椭圆内部,可求m的取值范围.
,利用点M必在椭圆内部,可求m的取值范围.解答:解:(1)设A(x1,y1),B(x2,y2),代入椭圆方程可得
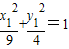 ,
,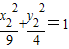
两式相减可得
 =
=
∵点M(1,1)为弦AB中点,∴
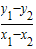 =-
=-
∴点M为弦AB中点时的直线l方程为y-1=-
 (x-1),即9y+4x-13=0
(x-1),即9y+4x-13=0(2)设弦AB的中点为(x,y),则由(1)知
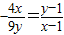 ,即9y2+4x2-9y-4x=0,∴弦AB的中点轨迹为椭圆;
,即9y2+4x2-9y-4x=0,∴弦AB的中点轨迹为椭圆;(3)(文)设弦AB的中点为(x,y),则由(1)知2=
 ,即9y+2x=0,∴弦AB的中点轨迹为直线;
,即9y+2x=0,∴弦AB的中点轨迹为直线;(理)设A,B的中点M为(x,y),kAB=
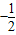 =
=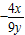 ①
①又中点M在直线l:y=2x+m上,y=2x+m②
由①②得:

点M必在椭圆内部,所以有
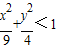
∴
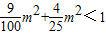
∴m2<4
解得:-2<m<2
点评:本题考查直线与圆锥曲线的综合,考查点差法的运用,考查对称性,解题的关键是正确运用点差法.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目