题目内容
设集合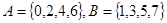 ,从集合
,从集合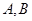 中各取2个元素组成没有重复数字的四位数.
中各取2个元素组成没有重复数字的四位数.
(1)可组成多少个这样的四位数?
(2)有多少个是2的倍数或是5的倍数?
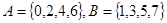 ,从集合
,从集合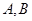 中各取2个元素组成没有重复数字的四位数.
中各取2个元素组成没有重复数字的四位数.(1)可组成多少个这样的四位数?
(2)有多少个是2的倍数或是5的倍数?
(1)756;(2)486.
第一问中利用先选后排,第一类,不含0:有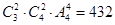 个,第二类,含0:有
个,第二类,含0:有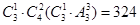 个,然后由分类加法计数原理知,共有432+324=756个符合条件的数。
个,然后由分类加法计数原理知,共有432+324=756个符合条件的数。
第二问中,利用因为是2的倍数即偶数,所以对于第一类,不含0:有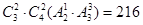 个,第二类,含0:有
个,第二类,含0:有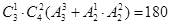 个,
个,
 共有216+180=396个;是5的倍数,只考虑末位数,即个位为5,同理有90个,解得。
共有216+180=396个;是5的倍数,只考虑末位数,即个位为5,同理有90个,解得。
解:(1)先选后排
第一类,不含0:有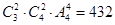 个,第二类,含0:有
个,第二类,含0:有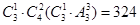 个,
个,
 由分类加法计数原理知,共有432+324=756个符合条件的数。
由分类加法计数原理知,共有432+324=756个符合条件的数。
(2).是2的倍数即偶数,
第一类,不含0:有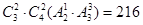 个,第二类,含0:有
个,第二类,含0:有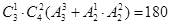 个,
个, 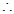 共有216+180=396个
共有216+180=396个
是5的倍数,只考虑末位数,即个位为5,同理有90个,
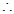 是2的倍数或者是5的倍数的无重复数字的四位数共有396+90=486个
是2的倍数或者是5的倍数的无重复数字的四位数共有396+90=486个
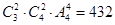 个,第二类,含0:有
个,第二类,含0:有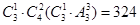 个,然后由分类加法计数原理知,共有432+324=756个符合条件的数。
个,然后由分类加法计数原理知,共有432+324=756个符合条件的数。第二问中,利用因为是2的倍数即偶数,所以对于第一类,不含0:有
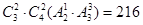 个,第二类,含0:有
个,第二类,含0:有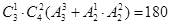 个,
个, 共有216+180=396个;是5的倍数,只考虑末位数,即个位为5,同理有90个,解得。
共有216+180=396个;是5的倍数,只考虑末位数,即个位为5,同理有90个,解得。解:(1)先选后排
第一类,不含0:有
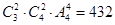 个,第二类,含0:有
个,第二类,含0:有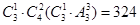 个,
个, 由分类加法计数原理知,共有432+324=756个符合条件的数。
由分类加法计数原理知,共有432+324=756个符合条件的数。 (2).是2的倍数即偶数,
第一类,不含0:有
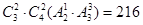 个,第二类,含0:有
个,第二类,含0:有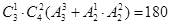 个,
个,  共有216+180=396个
共有216+180=396个是5的倍数,只考虑末位数,即个位为5,同理有90个,
 是2的倍数或者是5的倍数的无重复数字的四位数共有396+90=486个
是2的倍数或者是5的倍数的无重复数字的四位数共有396+90=486个
练习册系列答案
相关题目
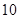 名队员中挑选
名队员中挑选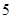 名上场比赛,要求甲、乙中至少有
名上场比赛,要求甲、乙中至少有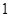 人参加,则下列选派方法种数表示不正确的是( ▲ )
人参加,则下列选派方法种数表示不正确的是( ▲ )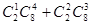
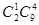
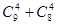
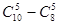

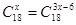 ,则
,则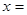 ▲ .
▲ . = .
= .