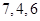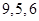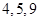题目内容
某校为了解高三学生在寒假期间的学习情况,抽查了100名同学,统计他们每天平均学习时间,绘成频率分布直方图(如图),则这100名同学中学习时间在6到8小时内的人数为 ( )
| A.50 | B.45 | C.40 | D.30 |
D
解析本题主要考查的是频率分布直方图。由条件可知2(0.04+0.12+x+0.14+0.05)=1,所以x=0.15.所以这100名同学中学习时间在6到8小时内的频率为0.15(10-8)=0.3=x/100,即x=30.应选D。

练习册系列答案
相关题目
已知某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图如图所示,则甲、乙两人得分的中位数之和是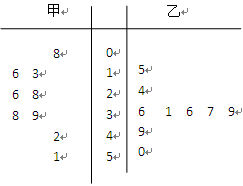
| A. 62 | B. 63 | C. 64 | D. 65 |
200辆汽车经过某一雷达地区,时速频率分布直方图如图所示,则时速超过60 km/h的汽车数量为( )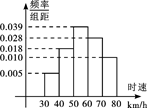
| A.70 | B.74 | C.76 | D.83 |
某校期末考试后,为了分析该校高一年级1000名学生的学习成绩,从中随机抽取了100名学生的成绩单,就这个问题来说,下面说法正确的是
| A.1000名学生是总体 | B.每个学生是个体 |
| C.100名学生的成绩是一个个体 | D.样本的容量是100 |
某单位有老年人27 人,中年人54人,青年人81人,为了调查他们的身体状况的某项指标,需从他们中间抽取一个容量为36的样本,则老年人、中年人、青年人分别各抽取的人数是( )
| A.6, 12 ,18 | B.7,11,19 | C.6,13,17 | D.7,12,17 |
如果 的方差为3,那么
的方差为3,那么 的方差是
的方差是
| A.0 | B.3 | C.6 | D.12 |
10名工人某天生产同一零件,生产的件数是15,17,14,10,15,17,17,16,14,12.设其平均数为a,中位数为b,众数为c,则有( ).
| A.a>b>c | B.b>c>a | C.c>a>b | D.c>b>a |
将一个总体为A,B,C三层后,其个体数之比为4:2:1,若用分层抽样的方法抽取容量为140的样本,则应从B层中抽取的个体数为 ( )
| A.20 | B.30 | C.40 | D.60 |
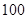 人,不到
人,不到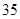 岁的有
岁的有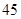 人,
人,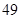 岁的
岁的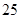 人,剩下的为
人,剩下的为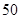 岁以上的人,现在抽取
岁以上的人,现在抽取 人进行分层抽样,各年龄段人数分别是
人进行分层抽样,各年龄段人数分别是