题目内容
将一个总体为A,B,C三层后,其个体数之比为4:2:1,若用分层抽样的方法抽取容量为140的样本,则应从B层中抽取的个体数为 ( )
| A.20 | B.30 | C.40 | D.60 |
D
解析

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
某校为了解高三学生在寒假期间的学习情况,抽查了100名同学,统计他们每天平均学习时间,绘成频率分布直方图(如图),则这100名同学中学习时间在6到8小时内的人数为 ( )
| A.50 | B.45 | C.40 | D.30 |
用秦九韶算法求多项式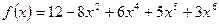 在
在 的值时,
的值时,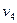 的值为 ( )
的值为 ( )
其中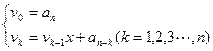
A. | B.576 | C. | D.536 |
样本中共有五个个体,其值分别为a,0,1,2,3,,若该样本的平均值为1,则样本方差为
A. | B. |
| C.2 | D. |
在对分类变量X, Y进行独立性检验时,算得 =7有以下四种判断
=7有以下四种判断
(p(K2>6.635)="0.010" )
(1) 有99﹪的把握认为X与Y有关;(2)有99﹪的把握认为X与Y无关;(3)在假设H0:X与Y 无关的前提下有99﹪的把握认为X与Y有关;(4)在假设H1: X与Y有关的前提下有99﹪的把握认为X与Y无关.以上4个判断正确的是 ( )
| A.(1)、(2) | B.(1)、(3) | C.(2)、(4) | D.(3)、(4) |
对变量x, y 有观测数据( ,
, )(i=1,2,…,10),得散点图1;对变量u ,v 有观测数据(
)(i=1,2,…,10),得散点图1;对变量u ,v 有观测数据( ,
, )(i=1,2,…,10),得散点图2. 由这两个散点图可以判断。
)(i=1,2,…,10),得散点图2. 由这两个散点图可以判断。 
图1 图2
| A.变量x 与y 正相关,u 与v 正相关 | B.变量x 与y 正相关,u 与v 负相关 |
| C.变量x 与y 负相关,u 与v 正相关 | D.变量x 与y 负相关,u 与v 负相关 |
某大学中文系共有本科生5 000人,期中一、二、三、四年级的学生比为5:4:3:1,要用分层抽样的方法从该系所有本科生中抽取一个容量为260的样本,则应抽二年级的学生
| A.100人 | B.60人 | C.80人 | D.20人 |
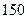 人,其中高级职称
人,其中高级职称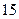 人,中级职称
人,中级职称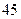 人,一般职员
人,一般职员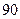 人,
人,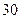 人进行分层抽样,则各职称人数分别为( )
人进行分层抽样,则各职称人数分别为( )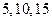
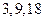
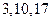
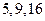
 测试成绩,得到样频率分布直方图如图所示,若满分为100分,规
测试成绩,得到样频率分布直方图如图所示,若满分为100分,规 定不低于60分为及格,则及格率是 ( )
定不低于60分为及格,则及格率是 ( )
