题目内容
(满分20分)本题有2小题,第1小题12分,第2小题8分.
设![]() 为定义域为
为定义域为![]() 的函数,对任意
的函数,对任意![]() ,都满足:
,都满足:![]() ,
,![]() ,且当
,且当![]() 时,
时,![]()
(1)请指出![]() 在区间
在区间![]() 上的奇偶性、单调区间、最大(小)值和零点,并运用相关定义证明你关于单调区间的结论;
上的奇偶性、单调区间、最大(小)值和零点,并运用相关定义证明你关于单调区间的结论;
(2)试证明![]() 是周期函数,并求其在区间
是周期函数,并求其在区间![]() 上的解析式.
上的解析式.
解:(1)偶函数; .………………………………………………………………………1分
最大值为2、最小值为0; .…………….……………………………………………………1分
单调递增区间:![]() ,单调递减区间:
,单调递减区间:![]() ...………………………………………1分
...………………………………………1分
零点:![]() . .…………………………..……………………………………………………1分
. .…………………………..……………………………………………………1分
单调区间证明:
当![]() 时,
时,![]()
设![]() ,
,![]() ,
,![]() ,
,
![]()
所以,![]() 在区间
在区间![]() 上是递减函数. ………………………………………………….4分
上是递减函数. ………………………………………………….4分
以下证明![]() 在区间
在区间![]() 上是递增函数.
上是递增函数.
【证明一】因为![]() 在区间
在区间![]() 上是偶函数.
上是偶函数.
对于任取的![]() ,
,![]() ,有
,有![]()
![]()
所以,![]() 在区间
在区间![]() 上是递增函数. ………………………………………………...4分
上是递增函数. ………………………………………………...4分
【证法二】设![]() ,由
,由![]() 在区间
在区间![]() 上是偶函数,得
上是偶函数,得
![]()
以下用定义证明![]() 在区间
在区间![]() 上是递增函数 ………………………………………..4分
上是递增函数 ………………………………………..4分
(2)设![]() ,
,![]() ,
,
所以,2是![]() 周期. ……………………………………………………………4分
周期. ……………………………………………………………4分
当![]() 时,
时,![]() ,
,
所以![]() 4分
4分

练习册系列答案
相关题目
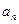 }和{
}和{ }满足:对于任何
}满足:对于任何 ,有
,有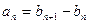 ,
, 为非零常数),且
为非零常数),且 .
. 是
是 与
与 的等差中项,试求
的等差中项,试求 的值,并研究:对任意的
的值,并研究:对任意的 }和{
}和{ }满足:对于任何
}满足:对于任何 ,有
,有 ,
, 为非零常数),且
为非零常数),且 .
. 是
是 与
与 的等差中项,试求
的等差中项,试求 的值,并研究:对任意的
的值,并研究:对任意的 为定义域为
为定义域为 的函数,对任意
的函数,对任意 ,都满足:
,都满足: ,
, ,且当
,且当 时,
时,
 上的奇偶性、单调区间、最大(小)值和零点,并运用相关定义证明你关于单调区间的结论;
上的奇偶性、单调区间、最大(小)值和零点,并运用相关定义证明你关于单调区间的结论; 上的解析式.
上的解析式.