题目内容
（满分20分）本题有2小题，第1小题12分，第2小题8分．
已知数列{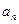
}和{
}满足：对于任何
，有
，
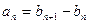为非零常数），且
．
（1）求数列{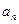}和{}的通项公式；
（2）若
是
与
的等差中项，试求
的值，并研究：对任意的，是否一定能是数列{}中某两项（不同于）的等差中项，并证明你的结论．
略
解析（1）【解一】由
得，
．
又
，
，
．
所以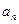，{}是首项为1，公比为的等比数列，
．…………………………….5分
由
，得
所以，当
时，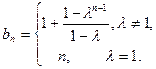
……………………………………………….6分
上式对
显然成立．………………………………………………………………………..1分
【解二】猜测，并用数学归纳法证明…………………………………………….5分的求法如【解一】 ………………………………………………………………………..7分
【解三】猜测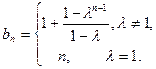，并用数学归纳法证明………………………….7分
…………………………………………………………………..5分
（2）当
时，不是与的等差中项，不合题意；……………………………….1分
当
时，由
得
，
由得
（可解得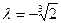
）..…………………………………………2分
对任意的
，是
与
的等差中项． .………………………………….2分
证明：
，
， .………………………………….3分
即，对任意的，是与的等差中项．
练习册系列答案
相关题目
}和{
}满足：对于任何
，有
，
为非零常数），且
．
是
与
的等差中项，试求
的值，并研究：对任意的
为定义域为
的函数，对任意
，都满足：
，
，且当
时，
上的奇偶性、单调区间、最大（小）值和零点，并运用相关定义证明你关于单调区间的结论；
上的解析式．
}和{
}满足：对于任何
，有
，
为非零常数），且
．
是
与
的等差中项，试求
的值，并研究：对任意的
为定义域为
的函数，对任意
，都满足：
，
，且当
时，
上的奇偶性、单调区间、最大（小）值和零点，并运用相关定义证明你关于单调区间的结论；
上的解析式．