题目内容
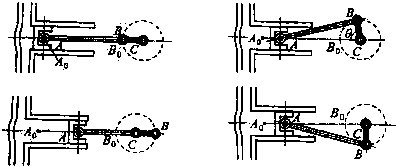
(2012•东莞二模)如图是曲柄连杆机构的示意图,当曲柄CB绕点C旋转时,通过连杆AB的传递,活塞作直线往复运动.当曲柄在CB0位置时,曲柄和连杆成一条直线,连杆的端点A在A0处,设连杆AB的长为lmm,曲柄CB的长为rmm,l>r.
(1)若l=300mm,r=80mm,当曲柄CB按顺时针方向旋转角为θ时,连杆的端点A此时离A0的距离为AA0=110mm,求cosθ的值;
(2)当曲柄CB按顺时针方向旋转角θ为任意角时,试用l、r、θ表示活塞移动的距离(即连杆的端点A移动的距离A0A)
(1)若l=300mm,r=80mm,当曲柄CB按顺时针方向旋转角为θ时,连杆的端点A此时离A0的距离为AA0=110mm,求cosθ的值;
(2)当曲柄CB按顺时针方向旋转角θ为任意角时,试用l、r、θ表示活塞移动的距离(即连杆的端点A移动的距离A0A)

分析:(1)在三角形中,利用余弦定理,可求cosθ的值;
(2)分类讨论,在△ABC中,由余弦定理,结合A0A=A0C-AC,即可求得结论.
(2)分类讨论,在△ABC中,由余弦定理,结合A0A=A0C-AC,即可求得结论.
解答:解:(1)由已知A0A=110mm时,可得AC=300+80-110=270.
又AB=l=300mm,BC=r=80mm
∴cosθ=
=
;
(2)设AC=x,若θ=0,则A0A=0;若θ=π,则A0A=2r
若0<θ<π,在△ABC中,由余弦定理,可得AB2=AC2+BC2-2AC•BCcosC
∴x2-2r(cosθ)x-(l2-r2)=0
∴x1=(rcosθ+
)(mm),x2=(rcosθ-
)<0(不合题意,舍去)
∴A0A=A0C-AC=(l+r-rcosθ-
)(mm)
若π<θ<2π,则根据对称性,将上式中的θ改为2π-θ即可,有
A0A=(l+r-rcosθ-
)(mm)
∴θ为任意角时,有A0A=(l+r-rcosθ-
)(mm).
又AB=l=300mm,BC=r=80mm
∴cosθ=
| AC2+BC2-AB2 |
| 2AC•BC |
| 107 |
| 432 |
(2)设AC=x,若θ=0,则A0A=0;若θ=π,则A0A=2r
若0<θ<π,在△ABC中,由余弦定理,可得AB2=AC2+BC2-2AC•BCcosC
∴x2-2r(cosθ)x-(l2-r2)=0
∴x1=(rcosθ+
| l2-r2sin2θ |
| l2-r2sin2θ |
∴A0A=A0C-AC=(l+r-rcosθ-
| l2-r2sin2θ |
若π<θ<2π,则根据对称性,将上式中的θ改为2π-θ即可,有
A0A=(l+r-rcosθ-
| l2-r2sin2θ |
∴θ为任意角时,有A0A=(l+r-rcosθ-
| l2-r2sin2θ |
点评:本题考查余弦定理的运用,考查三角模型的运用,考查学生的计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012•东莞二模)甲、乙两名运动员的5次测试成绩如图所示,设s1,s2分别表示甲、乙两名运动员测试成绩的标准差,
(2012•东莞二模)甲、乙两名运动员的5次测试成绩如图所示,设s1,s2分别表示甲、乙两名运动员测试成绩的标准差,