题目内容
从10位同学(其中6女,4男)中随机选出3位参加测验.每位女同学能通过测验的概率均为| 4 |
| 5 |
| 3 |
| 5 |
(I)选出的3位同学中,至少有一位男同学的概率;
(II)10位同学中的女同学甲和男同学乙同时被选中且通过测验的概率.
分析:(Ⅰ)由题意知本题是一个古典概型,试验发生的所有事件是从从10位同学中随机选出3位参加测验,满足条件的事件是选出的3位同学中至少有一位男同学,它的对立事件是选出的3位同学中没有男同学,根据对立事件的概率公式得到结果.
(2)由题意知本题是一个古典概型,试验发生的所有事件是从从10位同学(其中6女,4男)中随机选出3位参加测验,10位同学中的女同学甲和男同学乙同时被选中表示再从另外的八人中选一人,通过测验与被选中时相互独立事件同时发生的概率.
(2)由题意知本题是一个古典概型,试验发生的所有事件是从从10位同学(其中6女,4男)中随机选出3位参加测验,10位同学中的女同学甲和男同学乙同时被选中表示再从另外的八人中选一人,通过测验与被选中时相互独立事件同时发生的概率.
解答:解:(Ⅰ)由题意知本题是一个古典概型,
∵试验发生的所有事件是从从10位同学(其中6女,4男)中随机选出3位参加测验共有C103种结果,
满足条件的事件是选出的3位同学中至少有一位男同学,它的对立事件是选出的3位同学中没有男同学共有C63种结果,
∴根据古典概型的公式得到随机选出的3位同学中,至少有一位男同学的概率为1-
=
;
(Ⅱ)∵由题意知本题是一个古典概型,
∵试验发生的所有事件是从从10位同学(其中6女,4男)中随机选出3位参加测验共有C103种结果,
10位同学中的女同学甲和男同学乙同时被选中表示再从另外的八人中选一人,共有C81种结果,
∴10位同学中的女同学甲和男同学乙同时被选中的概率是
∴甲、乙被选中且能通过测验的概率为
×
×
=
.;
∵试验发生的所有事件是从从10位同学(其中6女,4男)中随机选出3位参加测验共有C103种结果,
满足条件的事件是选出的3位同学中至少有一位男同学,它的对立事件是选出的3位同学中没有男同学共有C63种结果,
∴根据古典概型的公式得到随机选出的3位同学中,至少有一位男同学的概率为1-
| ||
|
| 5 |
| 6 |
(Ⅱ)∵由题意知本题是一个古典概型,
∵试验发生的所有事件是从从10位同学(其中6女,4男)中随机选出3位参加测验共有C103种结果,
10位同学中的女同学甲和男同学乙同时被选中表示再从另外的八人中选一人,共有C81种结果,
∴10位同学中的女同学甲和男同学乙同时被选中的概率是
| ||
|
∴甲、乙被选中且能通过测验的概率为
| ||
|
| 4 |
| 5 |
| 3 |
| 5 |
| 4 |
| 125 |
点评:本小题主要考查组合,概率等基本概念,相互独立事件和互斥事件的概率以及运用概率知识解决实际问题的能力.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
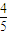 ,每位男同学能通过测验的概率均为
,每位男同学能通过测验的概率均为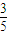 .试求:
.试求: