题目内容
直线![]() +
+![]() =1与椭圆
=1与椭圆![]() +
+![]() =1相交于A、B两点,椭圆上的点P使△PAB的面积等于12,这样的点P共有( )
=1相交于A、B两点,椭圆上的点P使△PAB的面积等于12,这样的点P共有( )
A.1个 B.2个 C.3个 D.4个
B
解析:
由△PAB的面积为12可知P到AB的距离为![]() =
=![]() ,
,
该题转化为椭圆上有多少个点P到直线AB的距离为![]() ,设P点坐标为(4cosθ,3sinθ),则P到AB的距离为
,设P点坐标为(4cosθ,3sinθ),则P到AB的距离为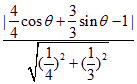 =
=![]()
![]() |
|![]() sin(θ+
sin(θ+![]() )-1|=2,
)-1|=2,
∴![]() sin(θ+
sin(θ+![]() )=3(舍去)或
)=3(舍去)或![]() sin(θ+
sin(θ+![]() )=-1
)=-1
![]() sin(θ+
sin(θ+![]() )=-
)=-![]() .
.
又0≤θ<2π,则![]() ≤θ+
≤θ+![]() <
<![]()
![]() θ+
θ+![]() =
=![]() 或θ+
或θ+![]() =
=![]() ,
,
即θ=π或θ=![]() .故有两个.
.故有两个.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目