题目内容
若函数 满足:在定义域内存在实数
满足:在定义域内存在实数 ,使
,使 (k为常数),则称“f(x)关于k可线性分解”.
(k为常数),则称“f(x)关于k可线性分解”.
(Ⅰ)函数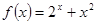 是否关于1可线性分解?请说明理由;
是否关于1可线性分解?请说明理由;
(Ⅱ)已知函数
 关于
关于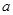 可线性分解,求
可线性分解,求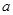 的取值范围;
的取值范围;
(Ⅲ)证明不等式:
 .
.
【答案】
(Ⅰ)是关于1可线性分解;(Ⅱ)a的取值范围是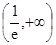 ;(Ⅲ)详见解析.
;(Ⅲ)详见解析.
【解析】
试题分析:(Ⅰ)函数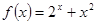 是否关于1可线性分解,关键是看是否存在
是否关于1可线性分解,关键是看是否存在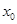 使得
使得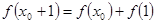 成立,若成立,是关于1可线性分解,否则不是关于1可线性分解,故看
成立,若成立,是关于1可线性分解,否则不是关于1可线性分解,故看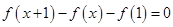 是否有解,构造函数
是否有解,构造函数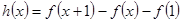 ,看它是否有零点,而
,看它是否有零点,而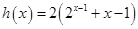 ,观察得
,观察得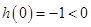 ,
,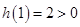 ,有根的存在性定理可得存在
,有根的存在性定理可得存在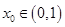 ,使
,使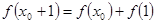 ;(Ⅱ)先确定定义域为
;(Ⅱ)先确定定义域为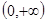 ,函数
,函数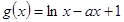
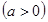 关于
关于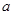 可线性分解,即存在
可线性分解,即存在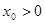 ,使
,使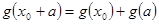 ,即
,即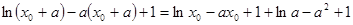 有解,整理得
有解,整理得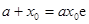 有解,即
有解,即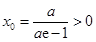 ,从而求出
,从而求出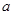 的取值范围;(Ⅲ)证明不等式:
的取值范围;(Ⅲ)证明不等式: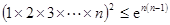 ,当
,当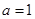 时,
时,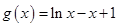 ,对
,对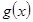 求导,判断最大值为
求导,判断最大值为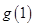 ,可得
,可得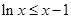 ,分别令
,分别令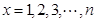 ,叠加可得证结论.
,叠加可得证结论.
试题解析:(Ⅰ)函数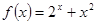 的定义域是R,若是关于1可线性分解,
的定义域是R,若是关于1可线性分解,
则定义域内存在实数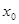 ,使得
,使得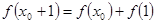 .
.
构造函数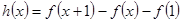
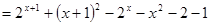
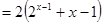 .
.
∵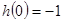 ,
,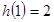 且
且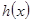 在
在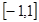 上是连续的,
上是连续的,
∴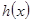 在
在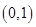 上至少存在一个零点.
上至少存在一个零点.
即存在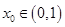 ,使
,使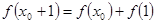 .
4分
.
4分
(Ⅱ)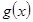 的定义域为
的定义域为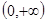 .
.
由已知,存在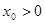 ,使
,使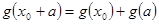 .
.
即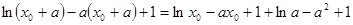 .
.
整理,得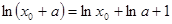 ,即
,即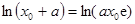 .
.
∴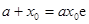 ,所以
,所以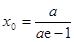 .
.
由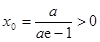 且
且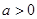 ,得
,得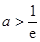 .
.
∴a的取值范围是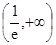 .
9分
.
9分
(Ⅲ)由(Ⅱ)知,a =1,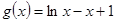 ,
,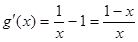 .
.
当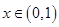 时,
时,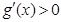 ,所以
,所以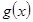 的单调递增区间是
的单调递增区间是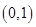 ,当
,当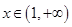 时,
时,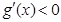 ,所以
,所以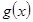 的单调递减区间是
的单调递减区间是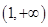 ,因此
,因此 时,
时,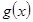 的最大值为
的最大值为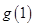 ,所以
,所以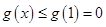 ,即
,即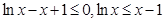 ,因此得:
,因此得: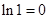 ,
,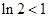 ,
,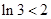 ,
, ,
,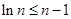 ,以上各式相加得:
,以上各式相加得: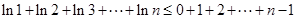 ,即
,即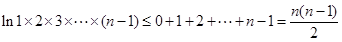 ,所以
,所以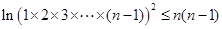 ,即
,即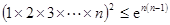
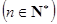 .
14分
.
14分
考点:导数在最大值、最小值问题中的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
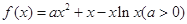 .
.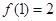 ,且在定义域内
,且在定义域内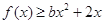 恒成立,求实数b的取值范围;
恒成立,求实数b的取值范围;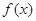 在定义域上是单调函数,求实数
在定义域上是单调函数,求实数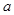 的取值范围;
的取值范围;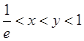 时,试比较
时,试比较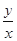 与
与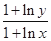 的大小.
的大小.