题目内容
商家通常依据“乐观系数准则”确定商品销售价格,即根据商品的最低销售限价a,最高销售限价b(b>a)以及实数x(0<x<1)确定实际销售价格c=a+x(b-a).这里x被称为乐观系数,经验表明,最佳乐观系数x恰好使得(c-a)是(b-c)和(b-a)的等比中项,某省为规范汽油市场,维护生产者的合法权益和消费者的长远利益,发改委发出通知,决定自9月28日零时起,0号柴油每升限价在[7.40,7.90]内(单位:元)
(1)试求出最佳乐观系数的值以及由此确定的0号柴油的销售价格(价格精确到0.01,参考值
≈2.24);
(2)某加油站老板做了一个市场调查后发现:若按最高销售限价出售则9月28号当天销售1500升,以后每天销售量将比前一天减少100升;若根据“乐观系数准则”确定柴油销售价格,每天的销售量稳定在1500升左右,若0号柴油的成本为每升7.01元,自9月28日起未来10天内加油站采用哪种销售价格出售将获利更多?
(1)试求出最佳乐观系数的值以及由此确定的0号柴油的销售价格(价格精确到0.01,参考值
| 5 |
(2)某加油站老板做了一个市场调查后发现:若按最高销售限价出售则9月28号当天销售1500升,以后每天销售量将比前一天减少100升;若根据“乐观系数准则”确定柴油销售价格,每天的销售量稳定在1500升左右,若0号柴油的成本为每升7.01元,自9月28日起未来10天内加油站采用哪种销售价格出售将获利更多?
分析:(1)根据题设条件,由(c-a)是(b-c)和(b-a)的等比中项,知[x(b-a)]2=(b-a)2-x(b-a)2,由此能求出最佳乐观系数x的值,从而可以求得0号柴油的销售价格;
(2)根据获利=销售收入-成本,分别按两种销售价格和销售量求解利润,比较即可得到答案.
(2)根据获利=销售收入-成本,分别按两种销售价格和销售量求解利润,比较即可得到答案.
解答:解:(1)∵c=a+x(b-a),即-c=-a-x(b-a),
∴b-c=(b-a)-x(b-a),①
∵(c-a)是(b-c)和(b-a)的等比中项,即(b-c)(b-a)=(c-a)2,
将①两边同乘以(b-a),可得(b-c)(b-a)=(b-a)2-x(b-a)2,即(c-a)2=(b-a)2-x(b-a)2,②
根据c=a+x(b-a),可得c-a=x(b-a),则(c-a)2=[x(b-a)]2,③
由②③可得,[x(b-a)]2=(b-a);-x(b-a)2,
∵b>a,则b-a>0,
∴x2+x-1=0,解得x=
,
∵0<x<1,
∴x=
∴最佳乐观系数x的值为
;
根据0号柴油每升限价在[7.40,7.90]内,则a=7.40,b=7.90,
∴0号柴油的销售价格为c=a+x(b-a)=7.40+
×(7.90-7.40)≈7.71元;
(2)按第一种方案销售,则自9月28日起未来10天内销售量为1500+1400+…+600=10500升,销售价格为最高销售限价7.90元,0号柴油的成本为每升7.01元,
则获利y1=(7.90-7.01)×10500=9345元;
按第二种方案销售,则自9月28日起未来10天内销售量为1500×10=15000升,根据“乐观系数准则”确定柴油销售价格为7.71元,0号柴油的成本为每升7.01元,
则获利y2=(7.71-7.01)×15000=10500元.
∵10500>9345,
∴自9月28日起未来10天内加油站采用第二种销售价格出售将获利更多,即按“乐观系数准则”确定柴油销售价格7.71元出售将获利更多.
∴b-c=(b-a)-x(b-a),①
∵(c-a)是(b-c)和(b-a)的等比中项,即(b-c)(b-a)=(c-a)2,
将①两边同乘以(b-a),可得(b-c)(b-a)=(b-a)2-x(b-a)2,即(c-a)2=(b-a)2-x(b-a)2,②
根据c=a+x(b-a),可得c-a=x(b-a),则(c-a)2=[x(b-a)]2,③
由②③可得,[x(b-a)]2=(b-a);-x(b-a)2,
∵b>a,则b-a>0,
∴x2+x-1=0,解得x=
-1±
| ||
| 2 |
∵0<x<1,
∴x=
-1+
| ||
| 2 |
∴最佳乐观系数x的值为
-1+
| ||
| 2 |
根据0号柴油每升限价在[7.40,7.90]内,则a=7.40,b=7.90,
∴0号柴油的销售价格为c=a+x(b-a)=7.40+
-1+
| ||
| 2 |
(2)按第一种方案销售,则自9月28日起未来10天内销售量为1500+1400+…+600=10500升,销售价格为最高销售限价7.90元,0号柴油的成本为每升7.01元,
则获利y1=(7.90-7.01)×10500=9345元;
按第二种方案销售,则自9月28日起未来10天内销售量为1500×10=15000升,根据“乐观系数准则”确定柴油销售价格为7.71元,0号柴油的成本为每升7.01元,
则获利y2=(7.71-7.01)×15000=10500元.
∵10500>9345,
∴自9月28日起未来10天内加油站采用第二种销售价格出售将获利更多,即按“乐观系数准则”确定柴油销售价格7.71元出售将获利更多.
点评:本题考查了函数在实际生产生活中的应用,解题的关键是正确的审题理解题意建立合适的数学模型,然后根据相关的数学知识解题.本题还考查了等比中项,等差数列求和的概念.属于难题.

练习册系列答案
相关题目
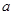 ,最高销售限价
,最高销售限价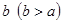 以及常数
以及常数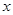 (
(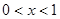 )确定实际销售价格
)确定实际销售价格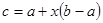 ,这里,
,这里,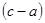 是
是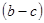 和
和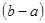 的等比中项,据此可得,最佳乐观系数
的等比中项,据此可得,最佳乐观系数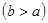 以及实数x
以及实数x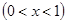 确定实际销售价格
确定实际销售价格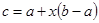 ,这里x被称为乐观系数。经验表明,最佳乐观系数x恰好使得
,这里x被称为乐观系数。经验表明,最佳乐观系数x恰好使得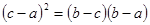 ,据此可得最佳乐观系数x的值为
,据此可得最佳乐观系数x的值为