题目内容
第(1)小题满分4分,第(2)小题满分6分,第(3)小题满分8分.
如果存在常数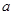 使得数列
使得数列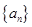 满足:若
满足:若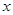 是数列
是数列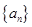 中的一项,则
中的一项,则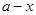 也是数列
也是数列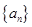 中的一项,称数列
中的一项,称数列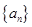 为“兑换数列”,常数
为“兑换数列”,常数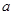 是它的“兑换系数”.
是它的“兑换系数”.
(1)若数列: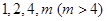 是“兑换系数”为
是“兑换系数”为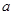 的“兑换数列”,求
的“兑换数列”,求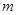 和
和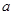 的值;
的值;
(2)已知有穷等差数列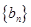 的项数是
的项数是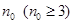 ,所有项之和是
,所有项之和是 ,求证:数列
,求证:数列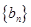 是“兑换数列”,并用
是“兑换数列”,并用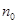 和
和 表示它的“兑换系数”;
表示它的“兑换系数”;
(3)对于一个不少于3项,且各项皆为正整数的递增数列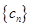 ,是否有可能它既是等比数列,又是“兑换数列”?给出你的结论并说明理由.
,是否有可能它既是等比数列,又是“兑换数列”?给出你的结论并说明理由.
(1)a=6,m=5;(2)见解析;(3)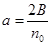
【解析】本试题主要考查了数列的运用。
解:(1)因为数列:1,2,4(m>4)是“兑换系数”为a的“兑换数列”
所以a-m,a-4,a-2,a-1也是该数列的项,且a-m<a-4<a-2<a-1-------------------1分
故a-m=1,a-4=2-------------------3分
即a=6,m=5 -------------------4分
(2)设数列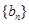 的公差为d,因为数列
的公差为d,因为数列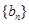 是项数为
是项数为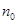 项的有穷等差数列
项的有穷等差数列
若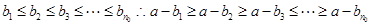
即对数列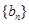 中的任意一项
中的任意一项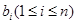
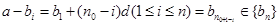 -------------------6分
-------------------6分
同理可得:若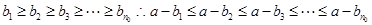 ,
,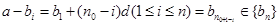 也成立,
也成立,
由“兑换数列”的定义可知,数列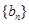 是
“兑换数列”;-------------------8分
是
“兑换数列”;-------------------8分
又因为数列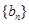 所有项之和是B,所以
所有项之和是B,所以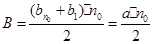 ,即
,即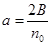 ------10分
------10分
(3)假设存在这样的等比数列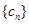 ,设它的公比为q,(q>1),
,设它的公比为q,(q>1),
因为数列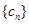 为递增数列,所以
为递增数列,所以
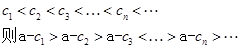
又因为数列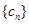 为“兑换数列”,则
为“兑换数列”,则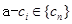 ,所以
,所以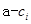 是正整数
是正整数
故数列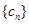 必为有穷数列,不妨设项数为n项,------------------12分
必为有穷数列,不妨设项数为n项,------------------12分
则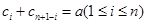 ----------14分
----------14分
① n=3则有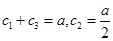 ,又
,又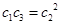 ,由此得q=1,与q>1矛盾;-------------------15分
,由此得q=1,与q>1矛盾;-------------------15分
②若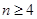 。由
。由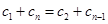 ,
,
即(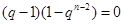 ),故q=1,与q>1矛盾;-------------------17分
),故q=1,与q>1矛盾;-------------------17分
综合①②得,不存在满足条件的数列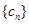 。-------------------18分
。-------------------18分

 阅读快车系列答案
阅读快车系列答案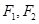 为双曲线
为双曲线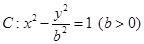 的左、右焦点,过
的左、右焦点,过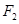 作垂直于
作垂直于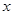 轴的直线,在
轴的直线,在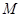 ,且
,且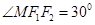 ,圆
,圆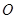 的方程为
的方程为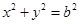 .
. 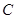 的方程;
的方程;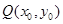 作切线
作切线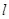 交双曲线
交双曲线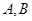 两个不同点,
两个不同点,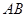 中点为
中点为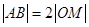 ;
;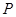 作两条渐近线的垂线,垂足分别是
作两条渐近线的垂线,垂足分别是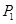 和
和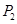 ,求
,求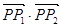 的值
的值 中,角
中,角 所对边的长分别为
所对边的长分别为 ,且
,且 .
. 的值;(2)求
的值;(2)求 的值.
的值. 写出与椭圆
写出与椭圆