题目内容
已知实数a,c分别为等比数列{an}的a1,a2,不等式-x2+6x-8>0 的解集为{x|a<x<c},则数列{an}的通项公式为
an=2n
an=2n
.分析:由题意可得a1,a2为方程-x2+6x-8=0的两实根,且a1<a2,解方程可得其值,进而可得公比,可得通项公式.
解答:解:由题意可得a1,a2为方程-x2+6x-8=0的两实根,且a1<a2,
解此方程可得x=2,或x=4,
∴a1=2,a2=4,或a1=4,a2=2(舍去)
∴等比数列{an}的公比q=
=
=2,
∴an=2×2n-1=2n,
故答案为:an=2n
解此方程可得x=2,或x=4,
∴a1=2,a2=4,或a1=4,a2=2(舍去)
∴等比数列{an}的公比q=
| a2 |
| a1 |
| 4 |
| 2 |
∴an=2×2n-1=2n,
故答案为:an=2n
点评:本题考查等比数列的通项公式,涉及一元二次不等式的解集,属基础题.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
 (2012•徐州模拟)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,
(2012•徐州模拟)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,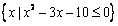 、B=
、B=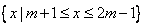 分别为函数
分别为函数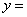 f(x)的定义域和值域, 且
f(x)的定义域和值域, 且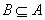 , 则实数m的取值范围是( ) A.
, 则实数m的取值范围是( ) A. 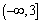 B.
B.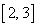 C.
C. 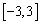 D.
D.