题目内容
定义:对函数y=f(x),对给定的正整数k,若在其定义域内存在实数x0,使得f(x0+k)=f(x0)+f(k),则称函数f(x)为“k性质函数”.
(1)若函数f(x)=2x为“1性质函数”,求x0;
(2)判断函数 是否为“k性质函数”?说明理由;
是否为“k性质函数”?说明理由;
(3)若函数 为“2性质函数”,求实数a的取值范围.
为“2性质函数”,求实数a的取值范围.
(本题满分(16分),第(1)小题(4分),第2小题(6分),第3小题6分)
解:(1)由f(x0+1)=f(x0)+f(1)得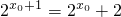 ,…(2分)
,…(2分)
∴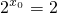 ,∴x0=1. …(4分)
,∴x0=1. …(4分)
(2)若存在x0满足条件,
则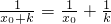 即
即 ,…(7分)
,…(7分)
∵△=k2-4k2=-3k2<0,∴方程无实数根,与假设矛盾.
∴ 不能为“k性质函数”. …(10分)
不能为“k性质函数”. …(10分)
(3)由条件得: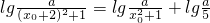 ,…(11分)
,…(11分)
即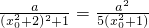 (a>0),
(a>0),
化简得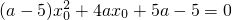 ,….(13分)
,….(13分)
当a=5时,x0=-1; …(14分)
当a≠5时,由△≥0,
16a2-20(a-5)(a-1)≥0即a2-30a+25≤0,
∴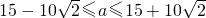 .
.
综上,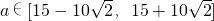 …(16分)
…(16分)
分析:做题时要紧扣新概念“k性质函数”(满足f(x0+k)=f(x0)+f(k)).
(1)由于函数f(x)=2x为“1性质函数”,则f(x0+1)=f(x0)+f(1),代入函数解析式可得x0的值;
(2)开放性命题,假设函数 是为“k性质函数”.则满足f(x0+k)=f(x0)+f(k)得到关于x0的二次方程,若方程有解,则函数f(x)=
是为“k性质函数”.则满足f(x0+k)=f(x0)+f(k)得到关于x0的二次方程,若方程有解,则函数f(x)= 是为“k性质函数”,若方程无解,则函数
是为“k性质函数”,若方程无解,则函数 不是为“k性质函数”;
不是为“k性质函数”;
(3)由于函数 为“2性质函数”,则f(x0+2)=f(x0)+f(2),代入解析式得到关于x0的二次方程,a为方程的参数,由于方程一定有解,得到关于a的不等式解出即可.
为“2性质函数”,则f(x0+2)=f(x0)+f(2),代入解析式得到关于x0的二次方程,a为方程的参数,由于方程一定有解,得到关于a的不等式解出即可.
点评:此题是个难题,考查创新概念及其应用,特别是问题(2)的设问形式,增加了题目的难度,综合性强.解决本题的灵魂在于“转化”,很多问题在实施“化难为易”、“化生为熟”中得以解决.求满足条件的参数的取值范围的题目是高考常考必考的.
解:(1)由f(x0+1)=f(x0)+f(1)得
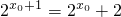 ,…(2分)
,…(2分)∴
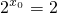 ,∴x0=1. …(4分)
,∴x0=1. …(4分)(2)若存在x0满足条件,
则
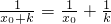 即
即 ,…(7分)
,…(7分)∵△=k2-4k2=-3k2<0,∴方程无实数根,与假设矛盾.
∴
 不能为“k性质函数”. …(10分)
不能为“k性质函数”. …(10分)(3)由条件得:
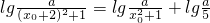 ,…(11分)
,…(11分)即
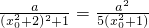 (a>0),
(a>0),化简得
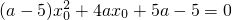 ,….(13分)
,….(13分)当a=5时,x0=-1; …(14分)
当a≠5时,由△≥0,
16a2-20(a-5)(a-1)≥0即a2-30a+25≤0,
∴
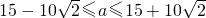 .
.综上,
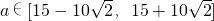 …(16分)
…(16分)分析:做题时要紧扣新概念“k性质函数”(满足f(x0+k)=f(x0)+f(k)).
(1)由于函数f(x)=2x为“1性质函数”,则f(x0+1)=f(x0)+f(1),代入函数解析式可得x0的值;
(2)开放性命题,假设函数
 是为“k性质函数”.则满足f(x0+k)=f(x0)+f(k)得到关于x0的二次方程,若方程有解,则函数f(x)=
是为“k性质函数”.则满足f(x0+k)=f(x0)+f(k)得到关于x0的二次方程,若方程有解,则函数f(x)= 是为“k性质函数”,若方程无解,则函数
是为“k性质函数”,若方程无解,则函数 不是为“k性质函数”;
不是为“k性质函数”;(3)由于函数
 为“2性质函数”,则f(x0+2)=f(x0)+f(2),代入解析式得到关于x0的二次方程,a为方程的参数,由于方程一定有解,得到关于a的不等式解出即可.
为“2性质函数”,则f(x0+2)=f(x0)+f(2),代入解析式得到关于x0的二次方程,a为方程的参数,由于方程一定有解,得到关于a的不等式解出即可.点评:此题是个难题,考查创新概念及其应用,特别是问题(2)的设问形式,增加了题目的难度,综合性强.解决本题的灵魂在于“转化”,很多问题在实施“化难为易”、“化生为熟”中得以解决.求满足条件的参数的取值范围的题目是高考常考必考的.

练习册系列答案
相关题目
 是否为“k性质函数”?说明理由;
是否为“k性质函数”?说明理由; 为“2性质函数”,求实数a的取值范围.
为“2性质函数”,求实数a的取值范围.