题目内容
(12分)定义运算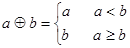 若函数
若函数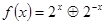 .
.
(1)求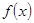 的解析式;
的解析式;
(2)画出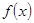 的图像,并指出单调区间、值域以及奇偶性.
的图像,并指出单调区间、值域以及奇偶性.
【答案】
(1)  ;(2)
;(2)
 在
在 上单调递增, 在
上单调递增, 在 上单调递减;值域为
上单调递减;值域为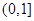
【解析】
试题分析:(1)根据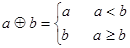 表示取a与b中较小的可知只需比较
表示取a与b中较小的可知只需比较 与
与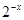 的大小关系即可得到结论.(2)由分段函数与指数函数性质画出图像,由图像可得出单调区间、值域以及奇偶性.
的大小关系即可得到结论.(2)由分段函数与指数函数性质画出图像,由图像可得出单调区间、值域以及奇偶性.
试题解析:
(1)由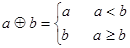 ,知
,知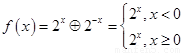
(2)  的图像如图:
的图像如图:

 在
在 上单调递增, 在
上单调递增, 在 上单调递减
上单调递减
值域为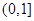
考点:函数解析式的求解及常用方法.

练习册系列答案
相关题目
对实数a与b,定义新运算“?”:a?b=
.设函数f(x)=(x2-2)?(x-1),x∈R.若函数y=f(x)-c的图象与x轴恰有两个公共点,则实数c的取值范围是( )
|
| A、(-1,1]∪(2,+∞) |
| B、(-2,-1]∪(1,2] |
| C、(-∞,-2)∪(1,2] |
| D、[-2,-1] |