题目内容
已知动点A(x,y)在圆x2+y2=1上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周,已知时间t=0时,点A(
,
),则0≤t≤12时,动点A的横坐标x关于t(单位:秒)的函数单调递减区间是( )
| 1 |
| 2 |
| ||
| 2 |
分析:点A的初始角为60°,当点A转过的角度在[60°,180°]或[360°,420°]时,动点A的横坐标x关于t的函数的单调递减再把角度区间转化为对应的时间区间,即可得到结论.
解答:解:t=0时,点A的坐标是(
,
),∴点A的初始角为60°,
当点A转过的角度在[60°,180°]或[360°,420°]时,动点A的横坐标x关于t的函数的单调递减,
∵12秒旋转一周,
∴每秒转过的角度是360°÷12=30°
∴当0≤t≤12时,动点A的横坐标x关于t的函数的单调递减是[0,4],[10,12]
故选D.
| 1 |
| 2 |
| ||
| 2 |
当点A转过的角度在[60°,180°]或[360°,420°]时,动点A的横坐标x关于t的函数的单调递减,
∵12秒旋转一周,
∴每秒转过的角度是360°÷12=30°
∴当0≤t≤12时,动点A的横坐标x关于t的函数的单调递减是[0,4],[10,12]
故选D.
点评:本题考查函数的单调性及单调区间,体现了转化的数学思想.

练习册系列答案
相关题目
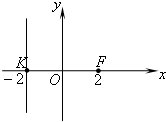 (2013•普陀区一模)已知动点A(x,y)到点F(2,0)和直线x=-2的距离相等.
(2013•普陀区一模)已知动点A(x,y)到点F(2,0)和直线x=-2的距离相等. ,求△AFK的面积.
,求△AFK的面积.
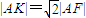 ,求△AFK的面积.
,求△AFK的面积.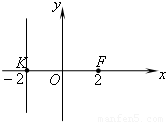
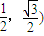 ,则0≤t≤12时,动点A的横坐标x关于t(单位:秒)的函数单调递减区间是( )
,则0≤t≤12时,动点A的横坐标x关于t(单位:秒)的函数单调递减区间是( )