题目内容
下列命题中,是正确的全称命题的是( )
| A、对任意的a∈R,都有a2-2a+1<0 | ||
| B、菱形的两条对角线相等 | ||
C、?x,
| ||
| D、对数函数在其定义域上是单调函数 |
分析:通过求二次函数的值域判断出A是假命题;通过菱形及矩形对角线的性质判断出B是假命题;通过含存在量词判断出C不是全称命题;通过对数函数的单调性判断出D是真命题.
解答:解:对于A,对任意a∈R,都有a2-2a+1≥0,所以A不正确
对于B,菱形的对角线垂直,矩形的对角线相等,故B不正确
对于C,此命题不是全称命题
对于D,是全称命题且是真命题
故选D
对于B,菱形的对角线垂直,矩形的对角线相等,故B不正确
对于C,此命题不是全称命题
对于D,是全称命题且是真命题
故选D
点评:判断一个命题是真命题还是假命题,一般利用所学的定义、性质、公里、定理等;判断一个命题是特称命题还是全称命题,关键看含着的量词.

练习册系列答案
相关题目
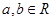 ,都有
,都有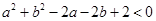 ;
;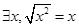 ;
; ,都有
,都有 ;
; 使得
使得 ;
;