题目内容
设向量 ,
, ,
, .
.(1)若
 ,求x的值;
,求x的值;(2)设函数
 ,求f(x)的最大值.
,求f(x)的最大值.
【答案】分析:(1)由条件求得 ,
, 的值,再根据
的值,再根据 以及x的范围,可的sinx的值,从而求得x的值.
以及x的范围,可的sinx的值,从而求得x的值.
(2)利用两个向量的数量积公式以及三角恒等变换化简函数f(x)的解析式为sin(2x- )+
)+ .结合x的范围,利用正弦函数的定义域和值域求得f(x)的最大值.
.结合x的范围,利用正弦函数的定义域和值域求得f(x)的最大值.
解答:解:(1)由题意可得 =
= +sin2x=4sin2x,
+sin2x=4sin2x, =cos2x+sin2x=1,
=cos2x+sin2x=1,
由 ,可得 4sin2x=1,即sin2x=
,可得 4sin2x=1,即sin2x= .
.
∵x∈[0, ],∴sinx=
],∴sinx= ,即x=
,即x= .
.
(2)∵函数 =(
=( sinx,sinx)•(cosx,sinx)=
sinx,sinx)•(cosx,sinx)= sinxcosx+sin2x=
sinxcosx+sin2x= sin2x+
sin2x+ =sin(2x-
=sin(2x- )+
)+ .
.
x∈[0, ],∴2x-
],∴2x- ∈[-
∈[-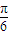 ,
, ],
],
∴当2x- =
= ,sin(2x-
,sin(2x- )+
)+ 取得最大值为 1+
取得最大值为 1+ =
= .
.
点评:本题主要考查两个向量的数量积的运算,三角函数的恒等变换及化简求值,正弦函数的定义域和值域,属于中档题.
 ,
, 的值,再根据
的值,再根据 以及x的范围,可的sinx的值,从而求得x的值.
以及x的范围,可的sinx的值,从而求得x的值.(2)利用两个向量的数量积公式以及三角恒等变换化简函数f(x)的解析式为sin(2x-
 )+
)+ .结合x的范围,利用正弦函数的定义域和值域求得f(x)的最大值.
.结合x的范围,利用正弦函数的定义域和值域求得f(x)的最大值.解答:解:(1)由题意可得
 =
= +sin2x=4sin2x,
+sin2x=4sin2x, =cos2x+sin2x=1,
=cos2x+sin2x=1,由
 ,可得 4sin2x=1,即sin2x=
,可得 4sin2x=1,即sin2x= .
.∵x∈[0,
 ],∴sinx=
],∴sinx= ,即x=
,即x= .
.(2)∵函数
 =(
=( sinx,sinx)•(cosx,sinx)=
sinx,sinx)•(cosx,sinx)= sinxcosx+sin2x=
sinxcosx+sin2x= sin2x+
sin2x+ =sin(2x-
=sin(2x- )+
)+ .
.x∈[0,
 ],∴2x-
],∴2x- ∈[-
∈[-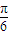 ,
, ],
],∴当2x-
 =
= ,sin(2x-
,sin(2x- )+
)+ 取得最大值为 1+
取得最大值为 1+ =
= .
.点评:本题主要考查两个向量的数量积的运算,三角函数的恒等变换及化简求值,正弦函数的定义域和值域,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,
, ,
,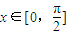 .
. ,求x的值;
,求x的值; ,求f(x)的最大值.
,求f(x)的最大值. ,
, ,
, .
. ∥
∥ ,求证:△ABC为等腰三角形;
,求证:△ABC为等腰三角形; ⊥
⊥ ,边长c=2,角C=
,边长c=2,角C= ,求△ABC的面积.
,求△ABC的面积. ,
, ,
, .
. ∥
∥ ,求证:△ABC为等腰三角形;
,求证:△ABC为等腰三角形; ⊥
⊥ ,边长c=2,角C=
,边长c=2,角C= ,求△ABC的面积.
,求△ABC的面积. ,
, ,
, .
. ∥
∥ ,求证:△ABC为等腰三角形;
,求证:△ABC为等腰三角形; ⊥
⊥ ,边长c=2,角C=
,边长c=2,角C= ,求△ABC的面积.
,求△ABC的面积.