题目内容
若椭圆的对称轴在坐标轴上，短轴的一个端点与两个焦点组成一个正三角形，焦点到椭圆上点的最短距离为
，则这个椭圆的方程为（ ）
| 3 |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
| D、以上都不对 |
分析：根据椭圆的基本概念与正三角形的性质，可得b=
c．再由椭圆焦点到椭圆上点的最短距离为a-c=
，联解得出a、b、c的值，即可得到所求椭圆的方程．
| 3 |
| 3 |
解答：
解：设短轴的一个端点为P，左右焦点分别为F1、F2，
∵△PF1F2为正三角形，
∴|OP|=
|F1F2|，可得b=
c，即
=
c．…①
又∵椭圆的焦点到椭圆上点的最短距离为
，
∴a-c=
，…②
联解①②，可得a=2
，c=
，b=
=3．
因此a2=12且b2=9，可得椭圆的标准方程为
+
=1或
+
=1．
故选：C
解：设短轴的一个端点为P，左右焦点分别为F1、F2，∵△PF1F2为正三角形，
∴|OP|=
| ||
| 2 |
| 3 |
| a2-c2 |
| 3 |
又∵椭圆的焦点到椭圆上点的最短距离为
| 3 |
∴a-c=
| 3 |
联解①②，可得a=2
| 3 |
| 3 |
| a2-c2 |
因此a2=12且b2=9，可得椭圆的标准方程为
| x2 |
| 12 |
| y2 |
| 9 |
| x2 |
| 9 |
| y2 |
| 12 |
故选：C
点评：本题已知椭圆满足的条件，求椭圆的标准方程．着重考查了正三角形的性质、椭圆的标准方程与简单几何性质等知识，属于中档题．
练习册系列答案
相关题目
：
可把平面直角坐标系上的一点
变换到这一平面上的一点
.
的中心为坐标原点，焦点在
轴上，且焦距为
，长轴顶点和短轴顶点间的距离为2. 求该椭圆
、
经变换公式
和
的坐标；
上一点
经变换公式
与点
：
可把平面直角坐标系上的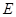点
变换到这一平面上的点
.特别地，若曲线
上一点
经变换公式
与点
的中心为坐标原点，焦点在
轴上，且焦距为
，长轴顶点和短轴顶点间的距离为2. 求该椭圆
时，其两个焦点
、
经变换公式
和
的坐标；
，
）下的不动点的存在情况和个数.
的中心在坐标原点、对称轴为坐标轴,且抛物线
的焦点是它的一个焦点,又点
在该椭圆上.
直线
与椭圆
,当
面积的最大值时，求直线
：
可把平面直角坐标系上的点
变换到这一平面上的点
.特别地，若曲线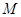
上一点
经变换公式
与点
的中心为坐标原点，焦点在
轴上，且焦距为
，长轴顶点和短轴顶点间的距离为2. 求该椭圆
时，其两个焦点
、
经变换公式
和
的坐标；
，
）下的不动点的存在情况和个数.
：
可把平面直角坐标系上的一点
变换到这一平面上的一点
.
的中心为坐标原点，焦点在
轴上，且焦距为
，长轴顶点和短轴顶点间的距离为2. 求该椭圆
、
经变换公式
和
的坐标；
上一点
经变换公式
与点