Question

（2012•许昌二模）已知圆锥的母线长为1，那么该圆锥体积的最大值为（　　）

• A．

  2 3 π

  27

• B．

  3 π

  24

• C．

  2 π

  12

• D．

  2 3 π

  9

Answer 1

分析：根据题意，可得圆锥底面半径r与高h的关系式：r²+h²=1，由此将圆锥的体积表示成关于r的函数，再将函数表达式中的被开方数凑成乘积为定值的形式，最后利用基本不等式求最值，即可求出求该圆锥体积的最大值．

解答：解：设圆锥底面半径为r，高为h，则圆锥体积V=

1

3

πr²•h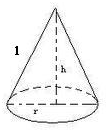
∵r²+h²=1，∴h=

1-r2

，
∴圆锥体积为
V=

1

3

πr²•

1-r2

=

2π

3

•

r2 2 • r2 2 (1-r2)

，
∵

r2

2

•

r2

2

•（1-r²）≤

( r2 2 + r2 2 +1-r2)

3

=

1

27

当且仅当

r2

2

=1-r²时，即当r=

6

3

时圆锥体积V取得最大值
∴该圆锥体积的最大值为V=

2π

3

•

1 27

=

2 3 π

27

故选：A

点评：本题给出母线长为定值的圆锥，求圆锥体积的最大值．着重考查了圆锥的体积公式和利用基本不等式求最值等知识点，属于中档题．