题目内容
7. 如图,E、F、G、H分别是空间四边形ABCD四边上的中点.
如图,E、F、G、H分别是空间四边形ABCD四边上的中点.(1)若BD=2,AC=6,则EG2+HF2等于多少?
(2)若AC与BD成30°的角,且AC=6,BD=4,则四边形EFGH的面积等于多少?
分析 (1)由题意得出四边形EFGH是平行四边形,求出它的各边长,再利用余弦定理求出EG2与HF2的表达式,即可得出EG2+HF2的值;
(2)根据平行线成角定理,再结合中位线定理,求出四边形EFGH的面积.
解答 解:(1)∵E、F、G、H分别是空间四边形ABCD四边上的中点,
∴EH∥BD,且EH=$\frac{1}{2}$BD;
FG∥BD,且FG=$\frac{1}{2}$BD;
∴EH∥FG,且EH=FG,
∴四边形EFGH是平行四边形;
又BD=2,AC=6,
∴EH=$\frac{1}{2}$BD=1,EF=$\frac{1}{2}$AC=3,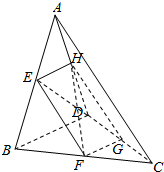
在△EFG和△HFG中,由余弦定理得,
EG2=EF2+FG2-2EF•FG•cos∠EFG
=32+12-2×3×1×cos∠EFG
=10-6cos∠EFG,
HF2=HG2+FG2-2HG•FG•cos∠FGH
=32+12-2×3×1×cos(π-∠EFG)
=10+6cos∠EFG,
∴EG2+HF2=20;
(2)∵AC与BD成30°的角,且EF∥AC,FG∥BD,
∴∠EFG=30°,
又AC=6,BD=4,
∴EF=$\frac{1}{2}$AC=3,FG=$\frac{1}{2}$BD=2;
∴四边形EFGH的面积为S=EF•FG•sin∠EFG=3×2×sin30°=3.
点评 本题考查了空间中的平行关系的应用问题,也考查了正弦和余弦定理的应用问题,是综合性题目.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
14.使奇函数f(x)=sin(2x+α)在[-$\frac{π}{4}$,0]上为减函数的α的值可以是( )
| A. | 0 | B. | $\frac{π}{2}$ | C. | π | D. | $\frac{3}{2}$π |
19.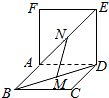 如图,两个正方形ABCD和ADEF所在平面互相垂直,设M、分别是BD和AE的中点,
如图,两个正方形ABCD和ADEF所在平面互相垂直,设M、分别是BD和AE的中点,
①AD⊥MN; ②MN∥面CDE;
③MN∥CE; ④MN、CE异面.
其中正确结论的个数是( )
 如图,两个正方形ABCD和ADEF所在平面互相垂直,设M、分别是BD和AE的中点,
如图,两个正方形ABCD和ADEF所在平面互相垂直,设M、分别是BD和AE的中点,①AD⊥MN; ②MN∥面CDE;
③MN∥CE; ④MN、CE异面.
其中正确结论的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
16.在等比数列{an}中,a1=-3,a2=-6,则a4的值为( )
| A. | -24 | B. | 24 | C. | ±24 | D. | -12 |
