题目内容
集合 ,
, ,
,
(Ⅰ)若 ,求
,求 的值;
的值;
(Ⅱ)若

 ,
,
 ,求
,求 的值.
的值.
 ,
, ,
,
(Ⅰ)若
 ,求
,求 的值;
的值;(Ⅱ)若


 ,
,
 ,求
,求 的值.
的值.(Ⅰ)5(Ⅱ)-2
本试题主要是考查而来集合的运算,以及集合间的关系的综合运用
(1)由于集合A,B,C表示的为一元二次方程的解,因此利用解集可知,要是满足题意,则2,3就是方程x2-ax+a2-19=0的两个根,得到a的值,
(2)由于空集是任何非空集合的真子集,可知集合A,B的交集不是空集,同时集合A,C交集为空集,得到参数a的值。
由已知,得B={2,3},C={2,-4}.
(Ⅰ)A∩B=A∪B, A=B
于是2,3是一元二次方程x2-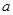 x+
x+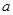 2-19=0的两个根,由韦达定理知:
2-19=0的两个根,由韦达定理知:
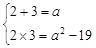 解之得
解之得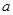 =5.
=5.
(Ⅱ)由A∩B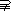

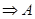 ∩
∩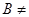
 ,又A∩C=
,又A∩C= ,得3∈A,2
,得3∈A,2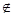 A,-4
A,-4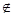 A,由3∈A,
A,由3∈A,
得32-3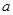 +
+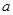 2-19=0,解得
2-19=0,解得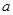 =5或
=5或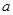 =-2
=-2
当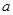 =5时,A={x|x2-5x+6=0}={2,3},与2
=5时,A={x|x2-5x+6=0}={2,3},与2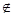 A矛盾;
A矛盾;
当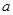 =-2时,A={x|x2+2x-15=0}={3,-5},符合题意.
=-2时,A={x|x2+2x-15=0}={3,-5},符合题意.
(1)由于集合A,B,C表示的为一元二次方程的解,因此利用解集可知,要是满足题意,则2,3就是方程x2-ax+a2-19=0的两个根,得到a的值,
(2)由于空集是任何非空集合的真子集,可知集合A,B的交集不是空集,同时集合A,C交集为空集,得到参数a的值。
由已知,得B={2,3},C={2,-4}.
(Ⅰ)A∩B=A∪B, A=B
于是2,3是一元二次方程x2-
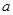 x+
x+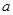 2-19=0的两个根,由韦达定理知:
2-19=0的两个根,由韦达定理知: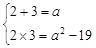 解之得
解之得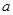 =5.
=5. (Ⅱ)由A∩B
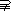

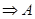 ∩
∩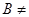
 ,又A∩C=
,又A∩C= ,得3∈A,2
,得3∈A,2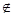 A,-4
A,-4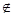 A,由3∈A,
A,由3∈A,得32-3
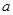 +
+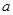 2-19=0,解得
2-19=0,解得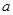 =5或
=5或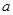 =-2
=-2当
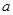 =5时,A={x|x2-5x+6=0}={2,3},与2
=5时,A={x|x2-5x+6=0}={2,3},与2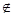 A矛盾;
A矛盾;当
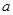 =-2时,A={x|x2+2x-15=0}={3,-5},符合题意.
=-2时,A={x|x2+2x-15=0}={3,-5},符合题意. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
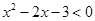 的解集为
的解集为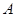 ,不等式
,不等式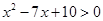 的解集为
的解集为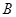 .
.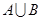 ;
; 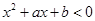 的解集为
的解集为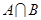 ,求
,求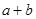 的值.
的值. ,
, ,求
,求 .
. ,集合
,集合 ,
, ,则实数
,则实数 的范围是 .
的范围是 .  ,
, ,若
,若 ,则
,则 的取值范围是( )
的取值范围是( )



 ,集合
,集合 ,则集合B中的元素有( )个
,则集合B中的元素有( )个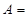 {x
{x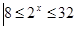 },
},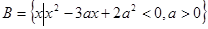 ,
,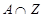 ; (2)若
; (2)若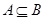 ,求
,求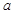 的取值范围。
的取值范围。 集合
集合 集合
集合 则
则 ( )
( )



 ,集合
,集合 ,
, ,则
,则