题目内容
观察下列三角形数表假设第n行的第二个数为an(n≥2,n∈N*).
(Ⅰ)依次写出第六行的所有6个数字;
(Ⅱ)归纳出an+1与an的关系式并求出an的通项公式;
(Ⅲ)设anbn=1,求证:b2+b3+…+bn<2.

【答案】分析:(I)根据三角形数表,两侧数为从1开始的自然数列,中间的数从第三行起,每一个数等于它两肩上的数之和的规律写出来.
(II)依据“中间的数从第三行起,每一个数等于它两肩上的数之和”则第二个数等于上一行第一个数与第二个数的和,即有an+1=an+n(n≥2),再由累加法求解.
(III)由anbn=1,解得 再由裂项相消法证明.
再由裂项相消法证明.
解答:解:(I)第六行的所有6个数字分别是
6,16,25,25,16,6;(2分)
(II)依题意an+1=an+n(n≥2),
a2=2an=a2+(a3-a2)+(a4-a3)++(an-an-1)
= ,
,
所以 ;
;
(III)因为anbn=1,所以 (12分)
(12分)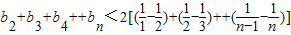 =
=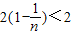 .(15分)
.(15分)
点评:本题通过三角数表构造了一系列数列,考查了数列的通项及求和的方法,还考查了数列间的关系,入题较难,知识点,方法活,属中档题.
(II)依据“中间的数从第三行起,每一个数等于它两肩上的数之和”则第二个数等于上一行第一个数与第二个数的和,即有an+1=an+n(n≥2),再由累加法求解.
(III)由anbn=1,解得
 再由裂项相消法证明.
再由裂项相消法证明.解答:解:(I)第六行的所有6个数字分别是
6,16,25,25,16,6;(2分)
(II)依题意an+1=an+n(n≥2),
a2=2an=a2+(a3-a2)+(a4-a3)++(an-an-1)
=
 ,
,所以
 ;
;(III)因为anbn=1,所以
 (12分)
(12分)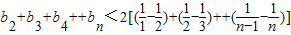 =
=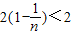 .(15分)
.(15分)点评:本题通过三角数表构造了一系列数列,考查了数列的通项及求和的方法,还考查了数列间的关系,入题较难,知识点,方法活,属中档题.

练习册系列答案
相关题目
 观察下列三角形数表
观察下列三角形数表 (n≥2,n∈N*).
(n≥2,n∈N*).
 与
与
