题目内容
已知长方形ABCD中,AB=4,BC=1,M为AB的中点,则在此长方形内随机取一点P,P与M的距离小于1的概率为( )
分析:以M点为圆心,以1为半径在长方形ABCD中作半圆,则该半圆内的任一点与M的距离小于1,以面积为测度,可求P与M的距离小于1的概率.
解答:解:以M点为圆心,以1为半径在长方形ABCD中作半圆,则该半圆内的任一点与M的距离小于1.
因此只要算出该半圆的面积占总面积的比例即为所求概率.
∵总面积=4×1=4,半圆面积=
π×1=
∴所求概率P=
=
故选C
因此只要算出该半圆的面积占总面积的比例即为所求概率.
∵总面积=4×1=4,半圆面积=
| 1 |
| 2 |
| π |
| 2 |
∴所求概率P=
| ||
| 4 |
| π |
| 8 |
故选C
点评:本题考查几何概型,考查概率的计算,确定以M点为圆心,以1为半径在长方形ABCD中作半圆,则该半圆内的任一点与M的距离小于1,是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


 折成直角二面角,且
折成直角二面角,且 .
.

 的体积.
的体积.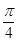 B.1-
B.1-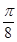 D.
D.