题目内容
已知a,b是方程4x2-4kx-1=0(k∈R)的两个不等实根,函数 的定义域为[a,b].
的定义域为[a,b].(1)当k=0时,求函数f(x)的值域;
(2)证明:函数f(x)在其定义域[a,b]上是增函数;
(3)在(1)的条件下,设函数
 ,若对任意的
,若对任意的 ,总存在
,总存在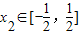 ,使得f(x2)=g(x1)成立,求实数m的取值范围.
,使得f(x2)=g(x1)成立,求实数m的取值范围.
【答案】分析:(1)确定函数解析式,求导函数,确定函数的单调性,从而可求函数f(x)的值域;
(2)确定函数在其定义域[a,b]上,导数为正,即可得到结论;
(3)由题意知:g(x)的值域是f(x)值域的子集,分别确定g(x)的值域、f(x)值域,即可求得实数m的取值范围.
解答:(1)解:当k=0时,4x2-1=0,∴x=± ,∴
,∴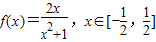 ,
,
∴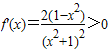 ,
,
∴f(x)在[ ]上单调递增
]上单调递增
∴函数f(x)的值域为[- ,
, ];
];
(2)证明:求导函数可得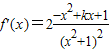
∵a,b是方程4x2-4kx-1=0(k∈R)的两个不等实根
∴抛物线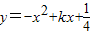 开口向下,两根之内的函数值必为正值
开口向下,两根之内的函数值必为正值
∵当x∈[a,b],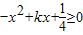 ,∴-x2+kx+1>0,
,∴-x2+kx+1>0,
∴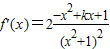 >0.
>0.
∴函数f(x)在其定义域[a,b]上是增函数;
(3)解:由题意知:g(x)的值域是f(x)值域的子集.
由(1)知,f(x)的值域是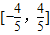 ,g'(x)=3x2-3m2,g'(x)=0⇒x=±m
,g'(x)=3x2-3m2,g'(x)=0⇒x=±m
显然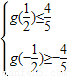 ,
,
∴欲使g(x)的值域是f(x)值域的子集,只需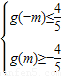 ,解得:
,解得: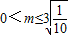 .
.
点评:本题考查导数知识的运用,考查函数的单调性与值域,考查学生分析解决问题的能力,属于中档题.
(2)确定函数在其定义域[a,b]上,导数为正,即可得到结论;
(3)由题意知:g(x)的值域是f(x)值域的子集,分别确定g(x)的值域、f(x)值域,即可求得实数m的取值范围.
解答:(1)解:当k=0时,4x2-1=0,∴x=±
 ,∴
,∴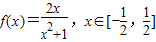 ,
,∴
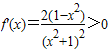 ,
,∴f(x)在[
 ]上单调递增
]上单调递增∴函数f(x)的值域为[-
 ,
, ];
];(2)证明:求导函数可得
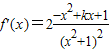
∵a,b是方程4x2-4kx-1=0(k∈R)的两个不等实根
∴抛物线
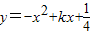 开口向下,两根之内的函数值必为正值
开口向下,两根之内的函数值必为正值∵当x∈[a,b],
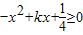 ,∴-x2+kx+1>0,
,∴-x2+kx+1>0,∴
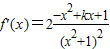 >0.
>0.∴函数f(x)在其定义域[a,b]上是增函数;
(3)解:由题意知:g(x)的值域是f(x)值域的子集.
由(1)知,f(x)的值域是
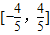 ,g'(x)=3x2-3m2,g'(x)=0⇒x=±m
,g'(x)=3x2-3m2,g'(x)=0⇒x=±m| x | 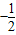 | 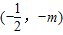 | -m | (-m,m) | m | 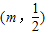 |  |
| f'(x) | + | - | + | ||||
| f(x) | 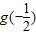 | 递增 | 极大值g(-m) | 递减 | 极小值g(m) | 递增 | 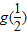 |
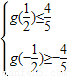 ,
,∴欲使g(x)的值域是f(x)值域的子集,只需
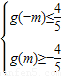 ,解得:
,解得: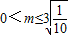 .
.点评:本题考查导数知识的运用,考查函数的单调性与值域,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 -4x+1 = 0的两个根,则(lg
-4x+1 = 0的两个根,则(lg )
)