题目内容
对于E={a1,a2,…,a100}的子集X=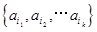 ,定义X的“特征数列”为x1,x2…,x100,其中
,定义X的“特征数列”为x1,x2…,x100,其中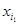 =
=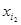 =…=
=…=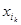 =1.其余项均为0,例如:子集{a2,a3}的“特征数列”为0,1,1,0,0,…,0.
=1.其余项均为0,例如:子集{a2,a3}的“特征数列”为0,1,1,0,0,…,0.
(1)子集{a1,a3,a5}的“特征数列”的前3项和等于 ;
(2)若E的子集P的“特征数列”p1,p2,…,p100满足p1=1,pi+pi+1=1,1≤i≤99;E的子集Q的“特征数列”q1,q2,…,q100满足q1=1,qj+qj+1+qj+2=1,1≤j≤98,则P∩Q的元素个数为 .
【答案】
(1)2 (2)17
【解析】(1)根据定义,子集{a1,a3,a5}的“特征数列”为1,0,1,0,1,0,0,…,0,共有3个1,其余全为0,该数列前3项和为2.
(2)E的子集P的“特征数列”p1,p2,…,p100中,由于p1=1,pi+pi+1=1(1≤i≤99),因此集合P中必含有元素a1.
又当i=1时,p1+p2=1,且p1=1,故p2=0.
同理可求得p3=1,p4=0,p5=1,p6=0,….
故E的子集P的“特征数列”为1,0,1,0,1,0,1,0,…,1,0,
即P={a1,a3,a5,a7,…,a99}.
用同样的方法求出Q={a1,a4,a7,a10,…,a100}.
因为1+3(n-1)=100,所以集合Q中有34个元素,下标是奇数的项有17个,
即P∩Q={a1,a7,a13,a19,…,a97},共有17个元素.

练习册系列答案
相关题目
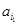 ,
,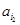 ,…,
,…, 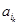 },定义X的“特征数列”
},定义X的“特征数列”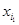 =
=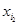 =…=
=…=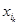 =1.其余项均为0,例如子集{a2,a3}的“特征数列”为0,1,0,0,…,0 子集{a1,a3,a5}的“特征数列”的前三项和等于________________;若E的子集P的“特征数列”P1,P2,…,P100满足P1+Pi+1="1,"
1≤i≤99;E 的子集Q的“特征数列” q1,q2,…,q100 满足q1=1,q1+qj+1+qj+2=1,1≤j≤98,则P∩Q的元素个数为___________.
=1.其余项均为0,例如子集{a2,a3}的“特征数列”为0,1,0,0,…,0 子集{a1,a3,a5}的“特征数列”的前三项和等于________________;若E的子集P的“特征数列”P1,P2,…,P100满足P1+Pi+1="1,"
1≤i≤99;E 的子集Q的“特征数列” q1,q2,…,q100 满足q1=1,q1+qj+1+qj+2=1,1≤j≤98,则P∩Q的元素个数为___________.