题目内容
已知双曲线C：
-y2=1,以C的右焦点为圆心且与其渐近线相切的圆方程为__________,若动点A，B分别在双曲线C的两条渐近线上，且
=2,则线段AB中点的轨迹方程为________.
(x-)2+y2=1，x2+16y2=4
解析：本题考查双曲线的几何性质以及轨迹方程的求法.已知双曲线方程为-y2=1，所以右焦点坐标为F(
,0)，渐近线方程为y=±
.所以以F为圆心与渐近线相切的圆的半径为点F到y=±
的距离，所以r=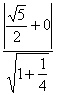
=1，所以圆的方程为：(x-
)2+y2=1.设A、B的坐标分别为(-a,2a)，(b,2b).中点M(x，y)，根据题意x=
=b+a,又|AB|=2，|AB|2=(a+b)2+4(a-b)2=4，∴4=x2+16y2，所以AB中点的轨迹方程为x2+16y2=4.
练习册系列答案
赢在课堂名师课时计划系列答案
天天向上课时同步训练系列答案
相关题目
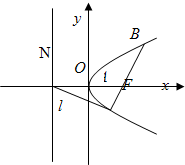已知双曲线C：y2-x2=8，直线l：y=-x+8，若椭圆M与双曲线C有公共焦点，与直线l有公共点P，求椭圆长轴的最小值及此时P点的坐标．
-y2=1,以C的右焦点为圆心且与其渐近线相切的圆方程为___________，定点（3，0）与C上动点距离的最小值为____________．
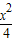-y2=1，P是C上的任意点．
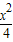-y2=1，P是C上的任意点．