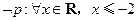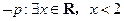题目内容
已知p:函数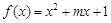 有两个零点,q:
有两个零点,q: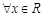 ,
,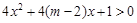 .若
.若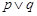 为真,
为真,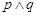 为假,则实数m的取值范围为
为假,则实数m的取值范围为
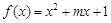 有两个零点,q:
有两个零点,q: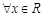 ,
,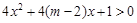 .若
.若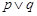 为真,
为真,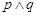 为假,则实数m的取值范围为
为假,则实数m的取值范围为A.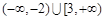 | B.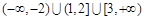 |
C. | D.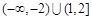 |
B
由p∨q为真,p∧q为假,知p,q有一个真命题一个假命题,由p得△=m2-4>0,解得m>2或m<-2.由q,得△=16(m-2)2-16<0,解得1<m<3,分两种情况求出实数m的取值范围.
解答:解:∵p∨q为真,p∧q为假
∴p,q中一个真命题一个假命题,
由p:函数f(x)=x2+mx+1有两个零点,
得△=m2-4>0,解得m>2或m<-2.
由q:?x∈R,4x2+4(m-2)x+1>0
得△=16(m-2)2-16<0,
解得1<m<3,
当p真q假时,有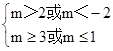 即m≥3或m<-2
即m≥3或m<-2
当p假q真,有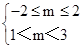
即1<m≤2
∴实数m的取值范围为(-∞,-2)∪(1,2]∪[3,+∞).
故选B.
解答:解:∵p∨q为真,p∧q为假
∴p,q中一个真命题一个假命题,
由p:函数f(x)=x2+mx+1有两个零点,
得△=m2-4>0,解得m>2或m<-2.
由q:?x∈R,4x2+4(m-2)x+1>0
得△=16(m-2)2-16<0,
解得1<m<3,
当p真q假时,有
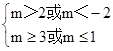 即m≥3或m<-2
即m≥3或m<-2当p假q真,有
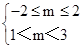
即1<m≤2
∴实数m的取值范围为(-∞,-2)∪(1,2]∪[3,+∞).
故选B.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
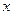 与
与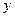 都是整数,就称点
都是整数,就称点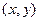 为整点,下列命题中正确的是_____________(写出所有正确命题的编号).
为整点,下列命题中正确的是_____________(写出所有正确命题的编号).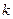 与
与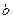 都是无理数,则直线
都是无理数,则直线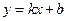 不经过任何整点
不经过任何整点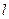 经过无穷多个整点,当且仅当
经过无穷多个整点,当且仅当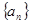 的前
的前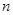 项和为
项和为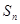 ,关于数列
,关于数列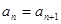 ;
;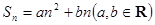 ,则数列
,则数列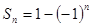 ,则数列
,则数列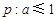 ,条件
,条件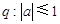 ,则
,则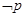 是
是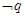 的
的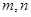 是两条不同的直线,
是两条不同的直线,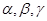 是三个不同的平面,则下列命题正确的是
是三个不同的平面,则下列命题正确的是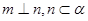 ,则
,则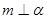 B 若
B 若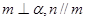 ,则
,则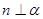
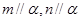 ,则
,则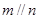 D 若
D 若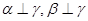 ,则
,则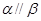
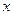 是方程
是方程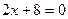 的根”此命题的否定是:
的根”此命题的否定是: 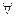 ”与“
”与“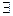 ”表示)
”表示)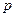 :
: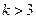 ;
;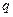 :方程
:方程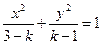 表示双曲线.则
表示双曲线.则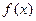 的定义域为D,若存在非零实数
的定义域为D,若存在非零实数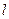 ,使得对于
,使得对于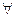
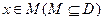 都有
都有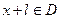 且
且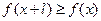 ,则称
,则称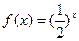 为R上的1高调函数;
为R上的1高调函数;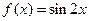 为R上的
为R上的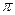
 高调函数;
高调函数;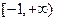 的函数
的函数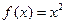 是
是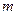 高调函数,则实数
高调函数,则实数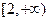 .
. 
 ,
, ,那么下列结论正确的是( ).
,那么下列结论正确的是( ).