题目内容
已知p:“直线x+y-m=0与圆(x-1)2+y2=1相交”;q:“mx2-x+m-4=0有一正根和一负根”,若p∨q为真,非p为真,求实数m的取值范围.
分析:先求出命题p,q的等价条件,然后利用若p∨q为真,非p为真,求实数m的取值范围.
解答:解:∵直线x+y-m=0与圆(x-1)2+y2=1相交,则
<1,
∴1-
<m<1+
,即p:1-
<m<1+
.
∵mx2-x+m-4=0有一正根和一负根,
则
<0,即0<m<4.即q:0<m<4.
又∵p∨q为真,非p为真,
∴p假,q真,即
,即1+
≤m<4.
∴m∈[1+
,4).
| |1+0-m| | ||
|
∴1-
| 2 |
| 2 |
| 2 |
| 2 |
∵mx2-x+m-4=0有一正根和一负根,
则
| m-4 |
| m |
又∵p∨q为真,非p为真,
∴p假,q真,即
|
| 2 |
∴m∈[1+
| 2 |
点评:本题主要考查复合命题的与简单命题的真假应用,将命题进行等价化简是解决此类问题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
 p 为真命题,求m的取值范围。
p 为真命题,求m的取值范围。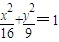 上任意一点,则|PQ|的最小值为 .
上任意一点,则|PQ|的最小值为 .