题目内容
甲乙两人独立解某一道数学题,已知该题被甲独立解出的概率为0.6,被甲、乙同时解出的概率为0.48,则该题被解出的概率为( )
分析:设“该题被甲独立解出”为事件A,“该题被乙独立解出”为事件B.由于被甲、乙同时解出的概率为0.48,由P(AB)=P(A)P(B),可得P(B),再利用P(A∪B)=P(A)+P(B)-P(AB)即可解出.
解答:解:设“该题被甲独立解出”为事件A,“该题被乙独立解出”为事件B,
∵被甲、乙同时解出的概率为0.48,且P(AB)=P(A)P(B),
∴0.48=0.6×P(B),解得P(B)=0.8.
∴该题被解出的概率P(A∪B)=P(A)+P(B)-P(AB)=0.6+0.8-0.48=0.92.
故选A.
∵被甲、乙同时解出的概率为0.48,且P(AB)=P(A)P(B),
∴0.48=0.6×P(B),解得P(B)=0.8.
∴该题被解出的概率P(A∪B)=P(A)+P(B)-P(AB)=0.6+0.8-0.48=0.92.
故选A.
点评:本题考查了事件的独立性计算公式、概率的加法计算公式,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
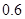 ,被甲或乙解出的概率为
,被甲或乙解出的概率为 ,(1)求该题被乙独立解出的概率;(2)求解出该题的人数
,(1)求该题被乙独立解出的概率;(2)求解出该题的人数 的数学期望和方差
的数学期望和方差 ,被甲或乙解出的概率为
,被甲或乙解出的概率为 ,(1)求该题被乙独立解出的概率;
,(1)求该题被乙独立解出的概率; 的数学期望和方差
的数学期望和方差