题目内容
设a,b,c∈R且a+b+c=1,求证a2+b2+c2≥ .
.
【答案】分析:利用条件,两边平方,利用基本不等式,即可证得结论.
解答:证明:∵a+b+c=1,
∴1=(a+b+c)2=a2+b2+c2+2(ab+bc+ac)≤3(a2+b2+c2),
∴a2+b2+c2≥ .
.
点评:本题考查不等式的证明,考查基本不等式的运用,考查学生分析解决问题的能力,属于中档题.
解答:证明:∵a+b+c=1,
∴1=(a+b+c)2=a2+b2+c2+2(ab+bc+ac)≤3(a2+b2+c2),
∴a2+b2+c2≥
 .
.点评:本题考查不等式的证明,考查基本不等式的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
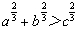 .
.