题目内容
设a、b、c∈R+且a+b=c，求证：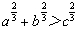
.
证明：∵a+b=c，∴
=1.又a、b、c∈R+，
∴0＜
＜1，0＜
＜1.
∴(
)
＞
，(
)
＞
.
∴(
)
+(
)
＞
+
=1.
∴.
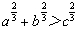练习册系列答案
走进文言文系列答案
相关题目
.
走进文言文系列答案题目内容
设a、b、c∈R+且a+b=c，求证：.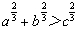
证明：∵a+b=c，∴=1.又a、b、c∈R+，
∴0＜＜1，0＜＜1.
∴()＞，()＞.
∴()+()＞+=1.
∴.
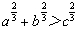走进文言文系列答案
-1)(
-1)(
-1),则必有( ) 
B.
≤M≤1
+b