题目内容
已知命题P:方程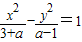 表示双曲线,命题q:点(2,a)在圆x2+(y-1)2=8的内部.若pΛq为假命题,¬q也为假命题,求实数a的取值范围.
表示双曲线,命题q:点(2,a)在圆x2+(y-1)2=8的内部.若pΛq为假命题,¬q也为假命题,求实数a的取值范围.
【答案】分析:根据双曲线的标准方程的特点把命题p转化为a>1或a<-3,根据点圆位置关系的判定把命题q转化为-1<a<3,根据pΛq为假命题,¬q也为假命题,最后取交集即可.
解答:解:∵方程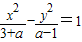 表示双曲线,
表示双曲线,
∴(3+a)(a-1)>0,解得:a>1或a<-3,
即命题P:a>1或a<-3;
∵点(2,a)在圆x2+(y-1)2=8的内部,
∴4+(a-1)2<8的内部,
解得:-1<a<3,
即命题q:-1<a<3,
由pΛq为假命题,¬q也为假命题,
∴实数a的取值范围是-1<a≤1.
点评:本题主要考查了双曲线的简单性质,以及点圆位置关系的判定方法.考查了学生分析问题和解决问题的能力.属中档题.
解答:解:∵方程
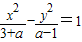 表示双曲线,
表示双曲线,∴(3+a)(a-1)>0,解得:a>1或a<-3,
即命题P:a>1或a<-3;
∵点(2,a)在圆x2+(y-1)2=8的内部,
∴4+(a-1)2<8的内部,
解得:-1<a<3,
即命题q:-1<a<3,
由pΛq为假命题,¬q也为假命题,
∴实数a的取值范围是-1<a≤1.
点评:本题主要考查了双曲线的简单性质,以及点圆位置关系的判定方法.考查了学生分析问题和解决问题的能力.属中档题.

练习册系列答案
相关题目
 是“方程
是“方程 ”表示椭圆的充要条件;
”表示椭圆的充要条件; 所表示的点在第二象限;
所表示的点在第二象限; 平面
平面 ,平面
,平面 ,则直线
,则直线 ,则下列复合命题中正确的是( )
,则下列复合命题中正确的是( )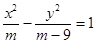 表示焦点在y轴上的椭圆;命题q:双曲线
表示焦点在y轴上的椭圆;命题q:双曲线 的离心率
的离心率 ,若p、q有且只有一个为真,求m的取值范围。
,若p、q有且只有一个为真,求m的取值范围。 表示焦点在y轴上的椭圆;
表示焦点在y轴上的椭圆; 的离心率
的离心率 ,若p、q有且只有一个为真,求m的取值范围.
,若p、q有且只有一个为真,求m的取值范围. 表示焦点在y轴上的椭圆;
表示焦点在y轴上的椭圆; 的离心率
的离心率 ;
; ”为真,“
”为真,“ ”为假,求实数
”为假,求实数 的取值范围.
的取值范围. 表示双曲线,命题q:点(
表示双曲线,命题q:点( ,
, )在圆
)在圆 的内部. 若
的内部. 若 为假命题,
为假命题, 也为假命题,求实数
也为假命题,求实数 的取值范围
的取值范围