题目内容
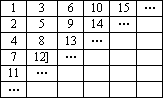
下面是一个向右和向下无限延伸的表格,将正整数按照表中已填数的规律填入:| 1 | 3 | 6 | 10 | 15 | |
| 2 | 5 | 9 | 14 | ||
| 4 | 8 | 13 | |||
| 7 | 12 | ||||
| 11 | |||||
A.6.58
B.6.57
C.7.58
D.7.57
【答案】分析:由已知表格中,数字的填写方式,第1行的数构成差值从2开始逐渐增加1的数列,即3-1=2,,6-3=3,10-6=4.15-10=5,…第2行的数构成差值从3开始逐渐增加1的数列,即5-2=3,9-5=4,14-9=5,…故第6行的数构成差值从7开始逐渐增加1的数列,由累加法可得通项,即可得到答案.
解答:解:分析表中数据,发现第6行的第1个数为16,
第1行的数构成差值从2开始逐渐增加1的数列,即3-1=2,,6-3=3,10-6=4.15-10=5,…
第2行的数构成差值从3开始逐渐增加1的数列,即5-2=3,9-5=4,14-9=5,…
…
故第6行的数构成差值从7开始逐渐增加1的数列,
可设第6行的数构成数列{an},且a1=16,a2-a1=7,a3-a2=8,a4-a3=9…an-an-1=n+5,
以上(n-1)个式子加起来,可得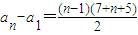 ,即an=
,即an=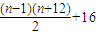 ,
,
令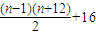 =2011,即n2+11n-4002=0,解得n=58或n=69(舍去)
=2011,即n2+11n-4002=0,解得n=58或n=69(舍去)
故2011出现在第6行,第58列
故选A
点评:本题重点考查归纳推理,其中根据已知表格中填写的数字,找出数字填写的规律是解答本题的关键.
解答:解:分析表中数据,发现第6行的第1个数为16,
第1行的数构成差值从2开始逐渐增加1的数列,即3-1=2,,6-3=3,10-6=4.15-10=5,…
第2行的数构成差值从3开始逐渐增加1的数列,即5-2=3,9-5=4,14-9=5,…
…
故第6行的数构成差值从7开始逐渐增加1的数列,
可设第6行的数构成数列{an},且a1=16,a2-a1=7,a3-a2=8,a4-a3=9…an-an-1=n+5,
以上(n-1)个式子加起来,可得
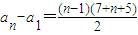 ,即an=
,即an=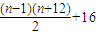 ,
,令
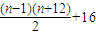 =2011,即n2+11n-4002=0,解得n=58或n=69(舍去)
=2011,即n2+11n-4002=0,解得n=58或n=69(舍去)故2011出现在第6行,第58列
故选A
点评:本题重点考查归纳推理,其中根据已知表格中填写的数字,找出数字填写的规律是解答本题的关键.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
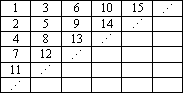
下面是一个向右和向下无限延伸的表格,将正整数按照表中已填数的规律填入:
则数2011在表中所处的行数和列数分别是( )
A.6.58
B.6.57
C.7.58
D.7.57
| 1 | 3 | 6 | 10 | 15 | |
| 2 | 5 | 9 | 14 | ||
| 4 | 8 | 13 | |||
| 7 | 12 | ||||
| 11 | |||||
A.6.58
B.6.57
C.7.58
D.7.57