题目内容
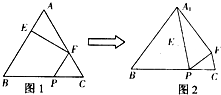 (2012•茂名一模)如图1,在正三角形ABC中,AB=3,E、F、P分别是AB、AC、BC边上的点,AE=CF=CP=1.将△AFE沿折起到△A1EF的位置,使平面A1EF与平面BCFE垂直,连接A1B、A1P(如图2).
(2012•茂名一模)如图1,在正三角形ABC中,AB=3,E、F、P分别是AB、AC、BC边上的点,AE=CF=CP=1.将△AFE沿折起到△A1EF的位置,使平面A1EF与平面BCFE垂直,连接A1B、A1P(如图2).(1)求证:PF∥平面A1EB;
(2)求证:平面BCFE⊥平面A1EB;
(3)求四棱锥A1-BPFE的体积.
分析:(1)证明PF∥平面A1EB,利用线面平行的判定定理,证明PF∥BE即可;
(2)证明平面BCFE⊥平面A1EB.利用面面垂直的判定定理,证明EF⊥平面A1EB即可;
(3)证明A1E⊥平面BCFE,即可求四棱锥A1-BPFE的体积.
(2)证明平面BCFE⊥平面A1EB.利用面面垂直的判定定理,证明EF⊥平面A1EB即可;
(3)证明A1E⊥平面BCFE,即可求四棱锥A1-BPFE的体积.
解答:(1)证明:∵CF=CP=x,CA=CB,∴PF∥BE
∵PF?平面A1BE,BE?平面A1BE
∴PF∥平面A1EB;
(2)证明:∵AE=1,AF=2,∠A=60°
∴EF=
,∴EF⊥A1E,EF⊥BE
∵A1E∩BE=E
∴EF⊥平面A1EB
∵EF?平面BCFE
∴平面BCFE⊥平面A1EB;
(3)∵平面A1EF与平面BCFE垂直,EF⊥A1E,平面A1EF与平面BCFE的交线为EF
∴A1E⊥平面BCFE
∵SEFPB=
(1+2)×
=
∵A1E=1
∴VA1-BPFE=
×
×1=
∵PF?平面A1BE,BE?平面A1BE
∴PF∥平面A1EB;
(2)证明:∵AE=1,AF=2,∠A=60°
∴EF=
| 3 |
∵A1E∩BE=E
∴EF⊥平面A1EB
∵EF?平面BCFE
∴平面BCFE⊥平面A1EB;
(3)∵平面A1EF与平面BCFE垂直,EF⊥A1E,平面A1EF与平面BCFE的交线为EF
∴A1E⊥平面BCFE
∵SEFPB=
| 1 |
| 2 |
| 3 |
3
| ||
| 2 |
∵A1E=1
∴VA1-BPFE=
| 1 |
| 3 |
3
| ||
| 2 |
| ||
| 2 |
点评:本题考查线面平行,面面垂直,考查四棱锥的体积计算.对于图形的翻折问题,关健是利用翻折前后的不变量.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
 (2012•茂名一模)如图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题:
(2012•茂名一模)如图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题: (2012•茂名一模)如图,设P是圆x2+y2=2上的动点,点D是P在x轴上的投影.M为线段PD上一点,且
(2012•茂名一模)如图,设P是圆x2+y2=2上的动点,点D是P在x轴上的投影.M为线段PD上一点,且