题目内容
已知函数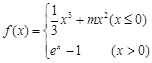
(1)讨论函数f (x)的极值情况;
(2)设g (x) =" ln(x" + 1),当x1>x2>0时,试比较f (x1 – x2)与g (x1 – x2)及g (x1) –g (x2)三者的大小;并说明理由.
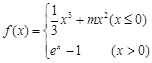
(1)讨论函数f (x)的极值情况;
(2)设g (x) =" ln(x" + 1),当x1>x2>0时,试比较f (x1 – x2)与g (x1 – x2)及g (x1) –g (x2)三者的大小;并说明理由.
(1)f (x)在(0, +∞)上递增,故f (x)有极小值f (0) = 0,f (x)有极大值 (2)见解析
(2)见解析
 (2)见解析
(2)见解析本试题主要考查了分段函数的极值的问题的运用。利用三次函数的极值的判定结合证明。以及利用单调性证明不等式的问题的综合运用。
(1)分别对于两段函数的单调性进行判定,确定极值问题。
(2)先对当x >0时,先比较ex – 1与ln(x + 1)的大小,
然后得到就是f (x) > g (x) ,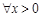 成立.再比较
成立.再比较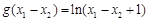 与g (x1) –g (x2) =ln(x1 + 1) –ln(x2 + 1)的大小.,利用作差法得到证明。
与g (x1) –g (x2) =ln(x1 + 1) –ln(x2 + 1)的大小.,利用作差法得到证明。
解:(1)当x>0时,f (x) = ex – 1在(0,+∞)单调递增,且f (x)>0;
当x≤0时,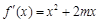 .
.
①若m = 0,f ′(x) = x2≥0, f (x) =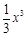 在(–∞,0]上单调递增,且f (x) =
在(–∞,0]上单调递增,且f (x) = .
.
又f (0) = 0,∴f (x)在R上是增函数,无极植;
②若m<0,f ′(x) = x(x + 2m) >0,则f (x) =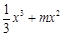 在(–∞,0)单调递增,同①可知f (x)在R上也是增函数,无极值; ………………4分
在(–∞,0)单调递增,同①可知f (x)在R上也是增函数,无极值; ………………4分
③若m>0,f (x)在(–∞,–2m]上单调递增,在(–2m,0)单调递减,
又f (x)在(0, +∞)上递增,故f (x)有极小值f (0) = 0,f (x)有极大值 . 6分
. 6分
(2)当x >0时,先比较ex – 1与ln(x + 1)的大小,
设h(x) = ex – 1–ln(x + 1) (x >0)
h′(x) =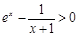 恒成立
恒成立
∴h(x)在(0,+∞)是增函数,h(x)>h (0) = 0
∴ex – 1–ln(x + 1) >0即ex – 1>ln(x + 1)
也就是f (x) > g (x) ,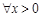 成立.
成立.
故当x1 – x2>0时,f (x1 – x2)> g (x1 – x2)……………………………10分
再比较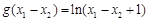 与g (x1) –g (x2) =ln(x1 + 1) –ln(x2 + 1)的大小.
与g (x1) –g (x2) =ln(x1 + 1) –ln(x2 + 1)的大小.
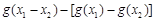 =
=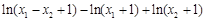
=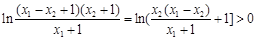
∴g (x1 – x2) > g (x1) –g (x2)
∴f (x1 – x2)> g (x1 – x2) > g (x1) –g (x2) .
(1)分别对于两段函数的单调性进行判定,确定极值问题。
(2)先对当x >0时,先比较ex – 1与ln(x + 1)的大小,
然后得到就是f (x) > g (x) ,
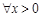 成立.再比较
成立.再比较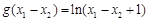 与g (x1) –g (x2) =ln(x1 + 1) –ln(x2 + 1)的大小.,利用作差法得到证明。
与g (x1) –g (x2) =ln(x1 + 1) –ln(x2 + 1)的大小.,利用作差法得到证明。解:(1)当x>0时,f (x) = ex – 1在(0,+∞)单调递增,且f (x)>0;
当x≤0时,
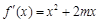 .
.①若m = 0,f ′(x) = x2≥0, f (x) =
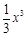 在(–∞,0]上单调递增,且f (x) =
在(–∞,0]上单调递增,且f (x) = .
.又f (0) = 0,∴f (x)在R上是增函数,无极植;
②若m<0,f ′(x) = x(x + 2m) >0,则f (x) =
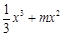 在(–∞,0)单调递增,同①可知f (x)在R上也是增函数,无极值; ………………4分
在(–∞,0)单调递增,同①可知f (x)在R上也是增函数,无极值; ………………4分③若m>0,f (x)在(–∞,–2m]上单调递增,在(–2m,0)单调递减,
又f (x)在(0, +∞)上递增,故f (x)有极小值f (0) = 0,f (x)有极大值
 . 6分
. 6分(2)当x >0时,先比较ex – 1与ln(x + 1)的大小,
设h(x) = ex – 1–ln(x + 1) (x >0)
h′(x) =
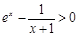 恒成立
恒成立∴h(x)在(0,+∞)是增函数,h(x)>h (0) = 0
∴ex – 1–ln(x + 1) >0即ex – 1>ln(x + 1)
也就是f (x) > g (x) ,
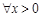 成立.
成立.故当x1 – x2>0时,f (x1 – x2)> g (x1 – x2)……………………………10分
再比较
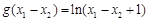 与g (x1) –g (x2) =ln(x1 + 1) –ln(x2 + 1)的大小.
与g (x1) –g (x2) =ln(x1 + 1) –ln(x2 + 1)的大小.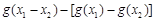 =
=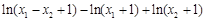
=
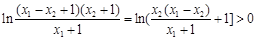
∴g (x1 – x2) > g (x1) –g (x2)
∴f (x1 – x2)> g (x1 – x2) > g (x1) –g (x2) .

练习册系列答案
相关题目
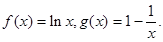
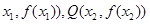 是函数 f(x)图象上任意两点,且0<x1<x2,若存在实数x3>0,使得
是函数 f(x)图象上任意两点,且0<x1<x2,若存在实数x3>0,使得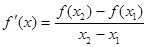 .请结合(I)中的结论证明:
.请结合(I)中的结论证明: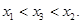
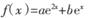 (a ,b
(a ,b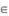 R,e为自然对数的底数),
R,e为自然对数的底数),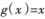 .
.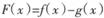 存在单调递增区间,求a的取值范围;
存在单调递增区间,求a的取值范围;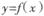 的图象C1与
的图象C1与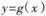 的图象C2相交于两个不同的点P、Q,过线段PQ的中点作x轴的垂线交C1于点
的图象C2相交于两个不同的点P、Q,过线段PQ的中点作x轴的垂线交C1于点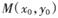 ,求证
,求证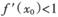 .
.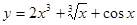 ,则导数
,则导数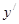 =( )
=( )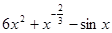
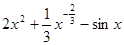
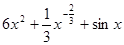

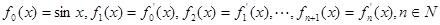 ,则
,则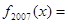 ( )
( )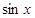
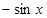
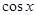
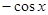
 在
在 处有极小值
处有极小值 ,
, 的值,并求出
的值,并求出 的单调区间.
的单调区间. 的方程
的方程 有3个不同实根,求实数a的取值范围.
有3个不同实根,求实数a的取值范围.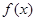 的导函数
的导函数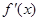 满足
满足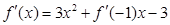 ,且
,且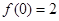 ,又
,又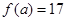 ,
,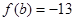 ,则
,则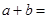 ( )
( ) 等于( )
等于( )


