题目内容
5.已知函数$f(x)=\left\{\begin{array}{l}{x^3},x≤0\\ x+\frac{1}{x}-3,x>0\end{array}\right.$,则f(f(1))=-1;若关于x的方程$f({x^2}+2x+\frac{1}{2})=m$有4个不同的实数根,则m的取值范围是m>0或-1<m<-$\frac{1}{8}$.分析 化简f(1)=1+1-3=-1,从而求f(f(1))=-1;作函数$f(x)=\left\{\begin{array}{l}{x^3},x≤0\\ x+\frac{1}{x}-3,x>0\end{array}\right.$的图象,分类讨论以确定方程的解的个数.
解答 解:f(1)=1+1-3=-1,
f(f(1))=f(-1)=(-1)3=-1;
作函数$f(x)=\left\{\begin{array}{l}{x^3},x≤0\\ x+\frac{1}{x}-3,x>0\end{array}\right.$的图象如下,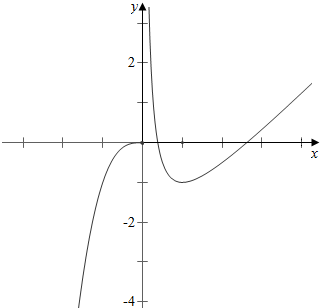 ,
,
当m<-1时,f(x)=m的解x∈(-∞,-1);
而x2+2x+$\frac{1}{2}$≥-$\frac{1}{2}$,
故方程$f({x^2}+2x+\frac{1}{2})=m$无解;
当m=-1时,f(x)=m的解为x=-1或x=1;
故x2+2x+$\frac{1}{2}$=-1或x2+2x+$\frac{1}{2}$=1;
故方程$f({x^2}+2x+\frac{1}{2})=m$有两个解;
当-1<m<-$\frac{1}{8}$时,
x2+2x+$\frac{1}{2}$=$\root{3}{m}$或x2+2x+$\frac{1}{2}$=x1,x2+2x+$\frac{1}{2}$=x2,
其中x1,x2是x+$\frac{1}{x}$-3=m的两个不同的解;
故x2+2x+$\frac{1}{2}$=$\root{3}{m}$无解,x2+2x+$\frac{1}{2}$=x1有两个不同的解,
x2+2x+$\frac{1}{2}$=x2有两个不同的解;
故方程$f({x^2}+2x+\frac{1}{2})=m$有四个不同的根;
当m=-$\frac{1}{8}$时,
x2+2x+$\frac{1}{2}$=-$\frac{1}{2}$或x2+2x+$\frac{1}{2}$=x1,x2+2x+$\frac{1}{2}$=x2,
其中x1,x2是x+$\frac{1}{x}$-3=-$\frac{1}{8}$的两个不同的解;
故x2+2x+$\frac{1}{2}$=-$\frac{1}{2}$有一个解,x2+2x+$\frac{1}{2}$=x1有两个不同的解,
x2+2x+$\frac{1}{2}$=x2有两个不同的解;
故方程$f({x^2}+2x+\frac{1}{2})=m$有5个不同的根;
当-$\frac{1}{8}$<m≤0时,
x2+2x+$\frac{1}{2}$=$\root{3}{m}$或x2+2x+$\frac{1}{2}$=x1,x2+2x+$\frac{1}{2}$=x2,
其中x1,x2是x+$\frac{1}{x}$-3=m的两个不同的解;
故x2+2x+$\frac{1}{2}$=$\root{3}{m}$有两个不同的解,x2+2x+$\frac{1}{2}$=x1有两个不同的解,
x2+2x+$\frac{1}{2}$=x2有两个不同的解;
故方程$f({x^2}+2x+\frac{1}{2})=m$有6个不同的根;
当m>0时,
x2+2x+$\frac{1}{2}$=x1或x2+2x+$\frac{1}{2}$=x2,
其中x1,x2是x+$\frac{1}{x}$-3=m的两个不同的解;
故x2+2x+$\frac{1}{2}$=x1有两个不同的解,x2+2x+$\frac{1}{2}$=x2有两个不同的解;
故方程$f({x^2}+2x+\frac{1}{2})=m$有4个不同的根.
综上所述,m>0或-1<m<-$\frac{1}{8}$;
故答案为:m>0或-1<m<-$\frac{1}{8}$.
点评 本题考查了分段函数.的应用及数形结合的思想应用,同时考查了分类讨论的思想应用.

| A. | {x|x∈R} | B. | {x|x≠2kπ+$\frac{2π}{3}$} | ||
| C. | {x|x$≠2kπ+\frac{4π}{3},k∈Z$} | D. | {x|x≠2kπ+$\frac{2}{3}$π且x≠2kπ+$\frac{4}{3}π$,k∈Z] |