题目内容
【题目】某圆拱桥的圆拱跨度为20 m，拱高为4 m.现有一船，宽10 m，水面以上高3 m，这条船能否从桥下通过？
【答案】可以从桥下通过
【解析】
建立适当平面直角坐标系，如图所示，得出A，B，P，D，E各点的坐标，设出圆的标准方程，将A，B，P坐标代入确定出这座圆拱桥的拱圆方程，把D横坐标代入求出纵坐标，与3比较即可作出判断.
建立如图所示的坐标系.依题意，有A(－10,0)，B(10,0)，P(0,4)，D(－5,0)，E(5,0).
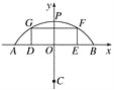
设所求圆的方程是(x－a)2＋(y－b)2＝r2(r＞0)，
于是有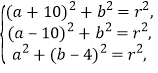
解此方程组，得a＝0，b＝－10.5，r＝14.5，
所以这座圆拱桥的拱圆的方程是x2＋(y＋10.5)2＝14.52(0≤y≤4).
把点D的横坐标x＝－5代入上式，得y≈3.1.
由于船在水面以上高3 m，3＜3.1，所以该船可以从桥下通过.
练习册系列答案
相关题目
【题目】某校乒乓球队有3名男同学A，B，C和3名女同学X，Y，Z，其年级情况如下表：
一年级 | 二年级 | 三年级 | |
男同学 | A | B | C |
女同学 | X | Y | Z |
现从这6名同学中随机选出2人参加乒乓球比赛（每人被选到的可能性相同）．
（1）用表中字母列举出所有可能的结果；
（2）设M为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”，求事件M发生的概率．
