题目内容
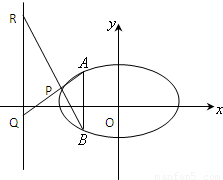
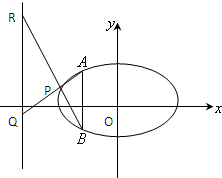
已知圆的方程为x2+y2=4,过点M(2,4)作圆的两条切线,切点分别为A1、A2,直线A1A2恰好经过椭圆 的右顶点和上顶点.
的右顶点和上顶点.(Ⅰ)求椭圆的方程;
(Ⅱ)设AB是椭圆
 (a>b>0)垂直于x轴的一条弦,AB所在直线的方程为x=m(|m|<a且m≠0),P是椭圆上异于A、B的任意一点,直线AP、BP分别交定直线
(a>b>0)垂直于x轴的一条弦,AB所在直线的方程为x=m(|m|<a且m≠0),P是椭圆上异于A、B的任意一点,直线AP、BP分别交定直线 于两点Q、R,求证
于两点Q、R,求证 .
.
【答案】分析:(Ⅰ)由图易求切点A1(2,0),根据MO⊥A1A2可求直线A1A2的方程,从而可求椭圆上顶点,进而得a,b值;
(Ⅱ)设P(x,y),A(m,n),B(m,-n),则有 ,m2+4n2-4=0,写出直线AP方程可求得yQ,同理求得yR,于是可得yQ•yR,进而得到
,m2+4n2-4=0,写出直线AP方程可求得yQ,同理求得yR,于是可得yQ•yR,进而得到
 ,再根据m的范围即可求证.
,再根据m的范围即可求证.
解答:解:(Ⅰ) 观察知,x=2是圆的一条切线,切点为A1(2,0),
设O为圆心,根据圆的切线性质,MO⊥A1A2,
所以 ,
,
所以直线A1A2的方程为 .
.
线A1A2与y轴相交于(0,1),依题意知a=2,b=1,
所求椭圆的方程为 .
.
(Ⅱ) 椭圆方程为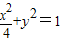 ,设P(x,y),A(m,n),B(m,-n),
,设P(x,y),A(m,n),B(m,-n),
则有 ,m2+4n2-4=0,
,m2+4n2-4=0,
在直线AP的方程 中,令
中,令 ,整理得
,整理得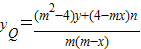 .①
.①
同理, .②
.②
①×②,并将 ,
, 代入得yQ•yR=
代入得yQ•yR=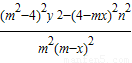
= =
=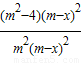 =
= .
.
而 =
= ,
,
∵|m|<2且m≠0,∴ ,
,
∴ .
.
点评:本题考查直线与圆锥曲线的位置关系,考查椭圆的标准方程,考查数形结合思想,考查学生的运算能力、分析问题解决问题的能力,难度较大.
(Ⅱ)设P(x,y),A(m,n),B(m,-n),则有
 ,m2+4n2-4=0,写出直线AP方程可求得yQ,同理求得yR,于是可得yQ•yR,进而得到
,m2+4n2-4=0,写出直线AP方程可求得yQ,同理求得yR,于是可得yQ•yR,进而得到
 ,再根据m的范围即可求证.
,再根据m的范围即可求证.解答:解:(Ⅰ) 观察知,x=2是圆的一条切线,切点为A1(2,0),
设O为圆心,根据圆的切线性质,MO⊥A1A2,
所以
 ,
,所以直线A1A2的方程为
 .
.线A1A2与y轴相交于(0,1),依题意知a=2,b=1,
所求椭圆的方程为
 .
.(Ⅱ) 椭圆方程为
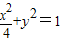 ,设P(x,y),A(m,n),B(m,-n),
,设P(x,y),A(m,n),B(m,-n),则有
 ,m2+4n2-4=0,
,m2+4n2-4=0,在直线AP的方程
 中,令
中,令 ,整理得
,整理得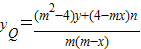 .①
.①同理,
 .②
.②①×②,并将
 ,
, 代入得yQ•yR=
代入得yQ•yR=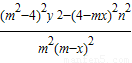
=
 =
=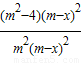 =
= .
.而
 =
= ,
,∵|m|<2且m≠0,∴
 ,
,∴
 .
.点评:本题考查直线与圆锥曲线的位置关系,考查椭圆的标准方程,考查数形结合思想,考查学生的运算能力、分析问题解决问题的能力,难度较大.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
已知圆的方程为x2+y2-6x-8y=0,设该圆过点(3,5)的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积为( )
A、10
| ||
B、20
| ||
C、30
| ||
D、40
|
 已知圆的方程为x2+y2=4,过点M(2,4)作圆的两条切线,切点分别为A1、A2,直线A1A2恰好经过椭圆
已知圆的方程为x2+y2=4,过点M(2,4)作圆的两条切线,切点分别为A1、A2,直线A1A2恰好经过椭圆