题目内容
已知函数f（x）在定义域（0．+∞）上是单调函数，若对于任意x∈（0，+∞），都有f（f（x）-
）=2，则f（
）的值是（ ）
| 1 |
| x |
| 1 |
| 5 |
分析：由函数f（x）在定义域（0，+∞）上是单调函数，且f（f（x）-
）=2，知f（x）-
为一个常数，令这个常数为n，则有f（x）-
=n，f（n）=2，所以n+
=2，解得n=1，由此能求出f（
）=6．
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 |
| n |
| 1 |
| 5 |
解答：解：∵函数f（x）在定义域（0，+∞）上是单调函数，
且f（f（x）-
）=2，
∴f（x）-
为一个常数，
令这个常数为n，则有f（x）-
=n，①
f（n）=2，②
由①得 f（x）=n+
，③
②代入③，得n+
=2，
解得n=1，
因此f（x）=1+
，
所以f（
）=6．
故选B．
且f（f（x）-
| 1 |
| x |
∴f（x）-
| 1 |
| x |
令这个常数为n，则有f（x）-
| 1 |
| x |
f（n）=2，②
由①得 f（x）=n+
| 1 |
| x |
②代入③，得n+
| 1 |
| n |
解得n=1，
因此f（x）=1+
| 1 |
| x |
所以f（
| 1 |
| 5 |
故选B．
点评：本题考查函数值的求法，是基础题．解题时要认真审题，仔细解答，注意合理地进行等价转化．
练习册系列答案
相关题目
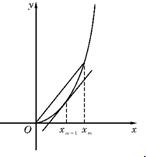已知函数f（x）=x3+x2，数列|xn|（xn＞0）的第一项xn=1，以后各项按如下方式取定：曲线x=f（x）在（xn+1，f（xn+1））处的切线与经过（0，0）和（xn，f （xn））两点的直线平行（如图）．
中ξi的选取是任意的，且In仅于n有关．