题目内容
下列说法正确的有( )个.①已知函数f(x)在(a,b)内可导,若f(x)在(a,b)内单调递增,则对任意的?x∈(a,b),有f′(x)>0.
②函数f(x)图象在点P处的切线存在,则函数f(x)在点P处的导数存在;反之若函数f(x)在点P处的导数存在,则函数f(x)图象在点P处的切线存在.
③因为3>2,所以3+i>2+i,其中i为虚数单位.
④定积分定义可以分为:分割、近似代替、求和、取极限四步,对求和
 中ξi的选取是任意的,且In仅于n有关.
中ξi的选取是任意的,且In仅于n有关.⑤已知2i-3是方程2x2+px+q=0的一个根,则实数p,q的值分别是12,26.
A.0
B.1
C.3
D.4
【答案】分析:利用导数的概念与几何意义可对①②作出判断,利用虚数不能比较大小可判断③,由定积分的定义可判断④,利用两复数相等的条件可判断⑤.
解答:解:①令f(x)=x3,则f(x)=x3在(-1,1)内单调递增,但当x=0时,f′(x)=0,故①错误;
②令f(x)=x3,函数f(x)在点P(0,0)处的导数存在,但函数f(x)图象在点P处的切线不存在,故②错误;
③由于虚数不能比较大小,故③错误;
④由定积分定义可知,In不仅与n有关,还与ξi的选取有关,故④错误;
⑤∵2i-3是方程2x2+px+q=0的一个根,
∴2(2i-3)2+p(2i-3)+q=0,
∴10-3p+q+(2p-24)i=0,
∴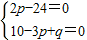 ,解得p=12,q=26.故⑤正确.
,解得p=12,q=26.故⑤正确.
综上所述,5个命题中只有一个命题正确.
故选B.
点评:本题考查命题的真假判断与应用,考查综合掌握知识、运用知识的能力,属于难题.
解答:解:①令f(x)=x3,则f(x)=x3在(-1,1)内单调递增,但当x=0时,f′(x)=0,故①错误;
②令f(x)=x3,函数f(x)在点P(0,0)处的导数存在,但函数f(x)图象在点P处的切线不存在,故②错误;
③由于虚数不能比较大小,故③错误;
④由定积分定义可知,In不仅与n有关,还与ξi的选取有关,故④错误;
⑤∵2i-3是方程2x2+px+q=0的一个根,
∴2(2i-3)2+p(2i-3)+q=0,
∴10-3p+q+(2p-24)i=0,
∴
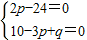 ,解得p=12,q=26.故⑤正确.
,解得p=12,q=26.故⑤正确.综上所述,5个命题中只有一个命题正确.
故选B.
点评:本题考查命题的真假判断与应用,考查综合掌握知识、运用知识的能力,属于难题.

练习册系列答案
相关题目