题目内容
【题目】已知椭圆![]() :
: ![]() (
(![]() )的左焦点为
)的左焦点为![]() ,离心率为
,离心率为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)设![]() 为坐标原点,
为坐标原点, ![]() 为直线
为直线![]() 上一点,过
上一点,过![]() 作
作![]() 的垂线交椭圆于
的垂线交椭圆于![]() ,
, ![]() .当四边形
.当四边形![]() 是平行四边形时,求四边形
是平行四边形时,求四边形![]() 的面积。
的面积。
【答案】(1) ![]() ;(2)
;(2)![]()
【解析】试题分析:(1)由已知得: ![]() ,
, ![]() ,所以
,所以![]() ,再由
,再由![]() 可得
可得![]() ,从而得椭圆的标准方程. )椭圆方程化为
,从而得椭圆的标准方程. )椭圆方程化为![]() .设PQ的方程为
.设PQ的方程为![]() ,代入椭圆方程得:
,代入椭圆方程得: ![]() .面积
.面积![]() ,而
,而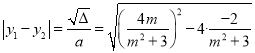 ,所以只要求出
,所以只要求出![]() 的值即可得面积.因为四边形OPTQ是平行四边形,所以
的值即可得面积.因为四边形OPTQ是平行四边形,所以![]() ,即
,即![]() .
.
再结合韦达定理即可得![]() 的值.
的值.
试题解析:(1)由已知得: ![]() ,
, ![]() ,所以
,所以![]()
又由![]() ,解得
,解得![]() ,所以椭圆的标准方程为:
,所以椭圆的标准方程为: ![]() .
.
(2)椭圆方程化为![]() .
.
设T点的坐标为![]() ,则直线TF的斜率
,则直线TF的斜率![]() .
.
当![]() 时,直线PQ的斜率
时,直线PQ的斜率![]() ,直线PQ的方程是
,直线PQ的方程是![]()
当![]() 时,直线PQ的方程是
时,直线PQ的方程是![]() ,也符合
,也符合![]() 的形式.
的形式.
将![]() 代入椭圆方程得:
代入椭圆方程得: ![]() .
.
其判别式![]() .
.
设![]() ,
,
则![]() .
.
因为四边形OPTQ是平行四边形,所以![]() ,即
,即![]() .
.
所以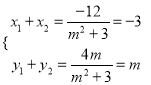 ,解得
,解得![]() .
.
此时四边形OPTQ的面积
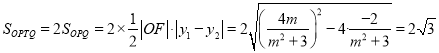 .
.

练习册系列答案
相关题目