题目内容
设A,B是锐角三角形的两个内角,则复数z=(ctgB-tanA)+(tanB-tanA)i对应点位于复平面的( )A.第一象限
B.第二象限
C.第三象限
D.第四象限
【答案】分析:先求复数对应的点的坐标,再对实部和虚部分别“切化弦”,进行通分后利用两角和(差)余弦公式进行化简,根据锐角三角函数的符号进行判断,再判断对应的点所在的象限.
解答:解:复数z=(cotB-tanA)+(tanB-cotA)i对应点为(cotB-tanA,tanB-cotA)
∵cotB-tanA=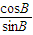 -
-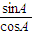 =
=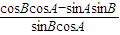 =
=
∵A,B是锐角,∴sinB>0,cosA>0,cos(A+B)<0,则cotB-tanA<0
∵tanB-cotA
=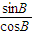 -
- =
=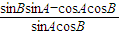 =-
=-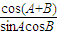
∵A,B是锐角,∴sinA>0,cosB>0,cos(A+B)<0,则tanB-cotA>0
所以复数Z对应的点位于复平面的第二象限,
故选B.
点评:本题考查了复数与复平面内对应点之间的关系,以及两角和(差)的余弦公式应用,三角函数在各个象限的符号.
解答:解:复数z=(cotB-tanA)+(tanB-cotA)i对应点为(cotB-tanA,tanB-cotA)
∵cotB-tanA=
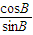 -
-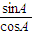 =
=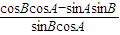 =
=
∵A,B是锐角,∴sinB>0,cosA>0,cos(A+B)<0,则cotB-tanA<0
∵tanB-cotA
=
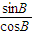 -
- =
=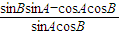 =-
=-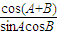
∵A,B是锐角,∴sinA>0,cosB>0,cos(A+B)<0,则tanB-cotA>0
所以复数Z对应的点位于复平面的第二象限,
故选B.
点评:本题考查了复数与复平面内对应点之间的关系,以及两角和(差)的余弦公式应用,三角函数在各个象限的符号.

练习册系列答案
相关题目